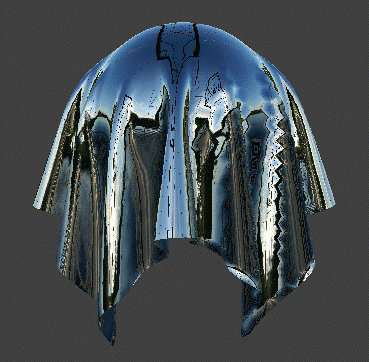CS 184: Computer Graphics and Imaging, Spring 2022

Project 4: Cloth Simulator

Alek Kozminski & Vincent Chiang, CS184-Simulators of the Cloth

Overview

In this project, we modeled a cloth as a collection of point masses connected by springs and simulated how said cloth would respond to different environmental conditions in different situations. We learned about simulating colliding objects, as well as how GSGL shaders work.

We found working as a team to be effective, as having two people able to look at the code made debugging much easier.

Note to people viewing on pdf: this document contains animated gifs that might not work on naive pdf, to view the full version please visit:

https://cal-cs184-student.github.io/sp22-project-webpages-rasterfarians/proj4/index.html

Part I: Masses and springs

scene/pinned2.json

... without any shearing constraints	... with only shearing constraints
... with all constraints

Part II: Simulation via numerical integration

Spring constant (ks) affects how much tension is in the cloth, which affects how much the cloth sags down, as well as the smoothness at steady state.

At high ks, there is more tension, and the cloth sags less, and is smooth at steady state. Additionally, at very high ks, there is so much tension in the cloth that it does not appear to be able to fall, and instead flails around almost horizontally.

At low ks, there is less tension, and the cloth sags more, and has more folds/creases at steady state.

scene/pinned2.json—default parameters with varying ks

ks = 50	ks = 5,000
ks = 50,000	ks = 500,000

Additionally, a video of the cloth with ks = 500,000:

Density affects how much the tension in the cloth affects the behavior of the cloth, in an inverse way to how the spring constant affects the behavior of the cloth (so decreasing density by a factor of 10 had the same effect as increasing ks by a factor of 10).

At low density, the tension on the cloth has a larger effect on it, and the cloth sags less, and is smooth at steady state. Additionally, at very low density, the tension in the cloth pulls it so much that it does not appear to be able to fall, and instead flails around almost horizontally.

At high density, the tension on the cloth has a smaller effect on it, and the cloth sags more, and has more folds/creases at steady state.

density = 1500	density = 15
density = 1.5	density = 0.15

Additionally, a video of the cloth with density = 0.15:

In summary, spring constant affects how much force is in the cloth, which affects the cloth's movement, while density affects how much the force in the cloth affects the cloth's movement in an equal and opposite way to the effect that the spring constant has on the cloth's movement.

Damping affects how fast the cloth falls, as well as how fast the cloth reaches steady state once it has fallen. At low damping, the cloth falls quickly, but swings for a while back and forth before coming to rest. At high damping, the cloth falls slowly, but very quickly stops swinging once it has fallen. At 0 damping, the cloth swings for a very long time (more than 5 minutes), and at 1 damping, the cloth stops swinging immediately.

From a physical standpoint, one would expect that at damping 0, energy in the cloth is completely conserved, and it should move forever. We believe that this may not be the case in our simulation because the position constraint in part 2.3 slowly saps energy from the cloth.

However, damping has no effect on the steady state position of the cloth.

damping = 0	damping = 0.2
damping = 1

scene/pinned4.json in its final resting state with default parameters

Part III: Handling collisions with other objects

ks = 500	ks = 5000
ks = 50000

With increasing ks, the number of folds in the cloth decreases, and the time the cloth takes to reach steady state increases.

The cloth on a plane at rest...
...with normal shading	...with custom (random noise) shading

Part IV: Handling self-collisions

The cloth folds in on itself less as it falls as spring constant increases, or as density decreases.

ks = 5,000, density = 15
Early stages	Middle stages
Final stages	Recording

ks = 50,000, density = 15
Early stages	Middle stages
Final stages	Recording

ks = 5000, density = 1.5
Early stages	Middle stages
Final stages	Recording

Part V: Shaders

Shader program controls and determines the positions, colors, and textures of objects in space. The vertex shader is responsible for the construction of vertices by computing their positions and other properties such as normals and tangents. The fragment shader is responsible for computing the color a vertex should take on to display the desired effect.

Task 1: Diffuse Shading

Diffuse-shaded sphere

Task 2: Blinn-Phong Shading

The Binn-Phong shading model is a technique in generating realistic 3D textures by combining ambient, diffuse, and specular lighting. Ambient lighting is constant, and its effect is experienced by every vertex in the scene. Diffuse lighting accounts for the direct lighting effect from a light source regardless of camera or viewing angle. Specular lighting is the reflected light or indirect illumination on an object in space with regards to camera or viewing angle.

ambient	diffuse
specular	all

Task 3: Texture Mapping

Texture-shaded Sphere with Custom Texture

Task 4: Displacement and Bump Mapping

For the images in this task, we used normal = 100 and height = 0.15. We used the provided texture_4.png.

Bump Mapping on Sphere	Displacement Mapping on Sphere
Bump Mapping on Cloth

Both mappings appear to have bumps, but upon closer inspection, the bump mapping is just different coloring, whereas displacement mapping simulates geometric bumps.

This can be seen in the shapes of the balls—the bump-mapped sphere maintains its shape, while the displacement-mapped sphere has a deformed shape with bumps. It should also be noted that the bump-mapped sphere actually is smaller than the displacement-mapped sphere, as the displacement-mapped sphere actually pushes the vertices outwards.

Bump Mapping on Sphere: Coarseness 16	Displacement Mapping on Sphere: Coarseness 16
Bump Mapping on Sphere: Coarseness 128	Displacement Mapping on Sphere: Coarseness 128

Changing the coarseness does not appear to change the way the bump shader shades the sphere. However, increasing the coarseness makes the displacement-mapped sphere slightly bigger, and makes the bumps look more jagged.

Task 5: Environment-mapped Reflections

Mirror Shading on Sphere	Mirror Shading on Cloth

Extra Credit: Custom Shading

We made a custom shading in which all color channels and the alpha value are random:

The sphere scene with our custom shading

We created this using a function that takes in a vec2 and generates a random float from it and calling it (with v_uv as input) to get all values of the out_color vector.

The function was fract(sin(dot(v_uv, vec2(12.9898, 78.233))) * 43758.5453)..

Link to website: https://cal-cs184-student.github.io/sp22-project-webpages-rasterfarians/proj4/index.html