
CS 184: Spring 2022
Sam Ellgass and Nima Rezaeian
In ClothSim, we used spring equations and the Verlet integration equation to model cloth as a network of springs in order to simulate movement, collision, and a variety of shading techniques.
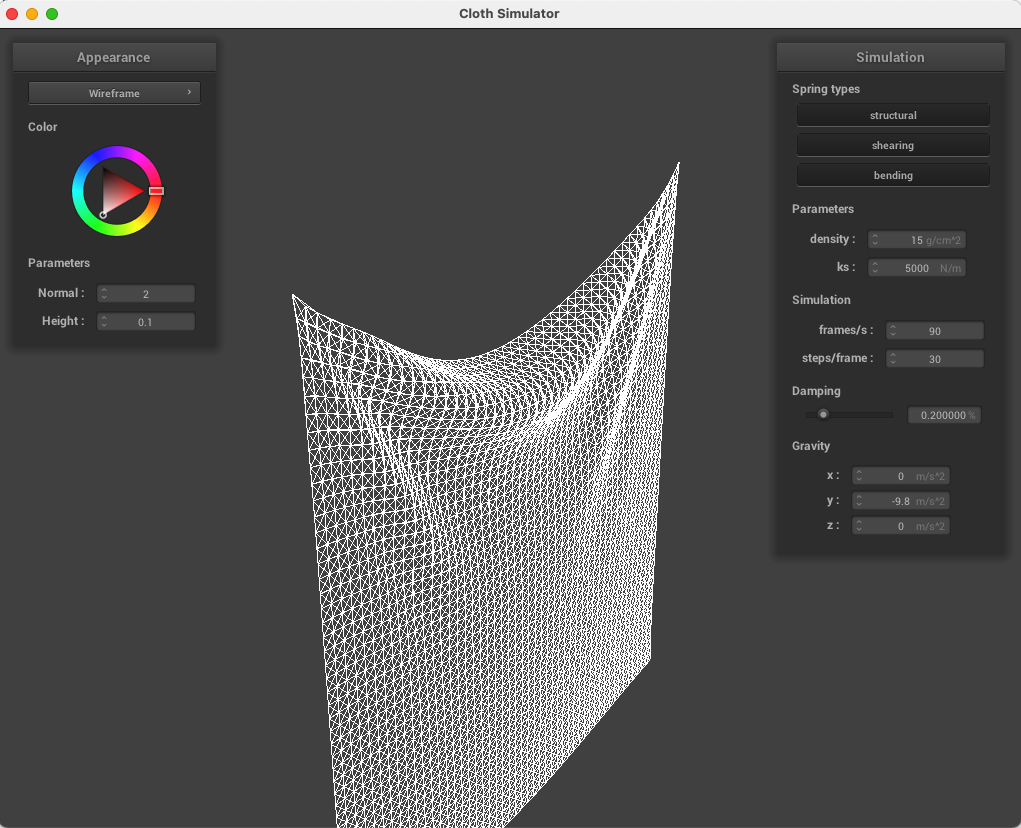
In this task, we implemented the "cloth" as a network of structural, shearing, and bending springs. Below, our cloth can be seen with falling from above with two corners pinned in place. The left image occurred earlier in simulation and the right image later.


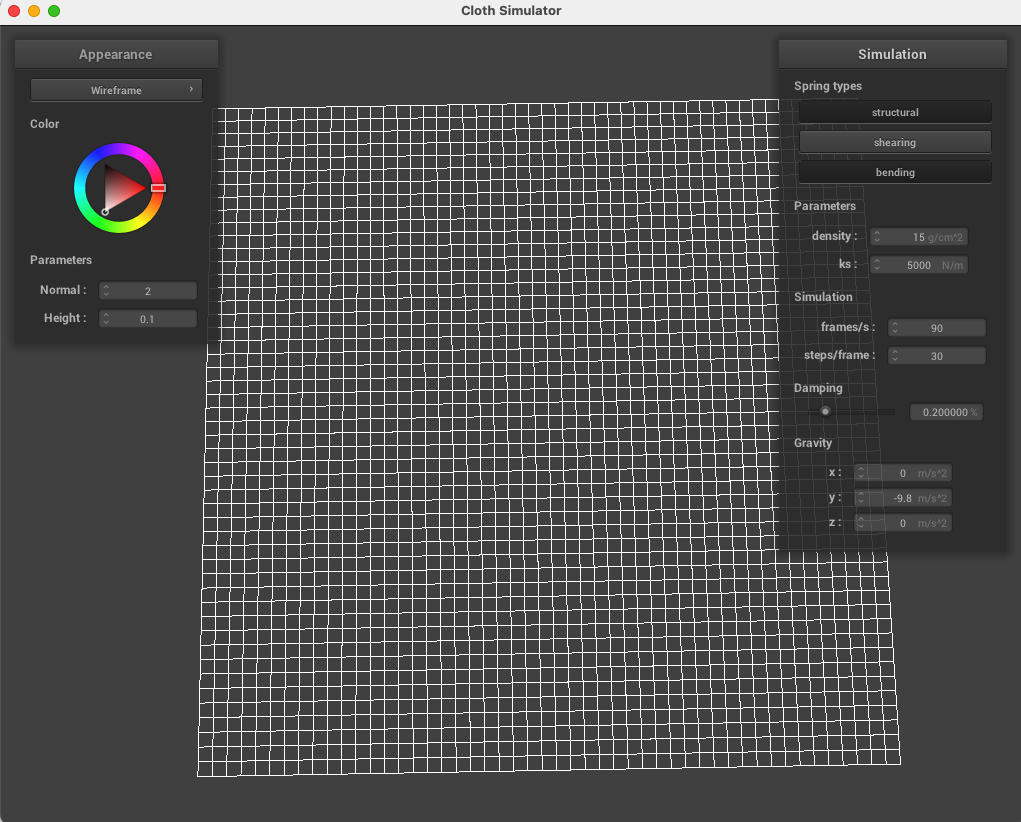
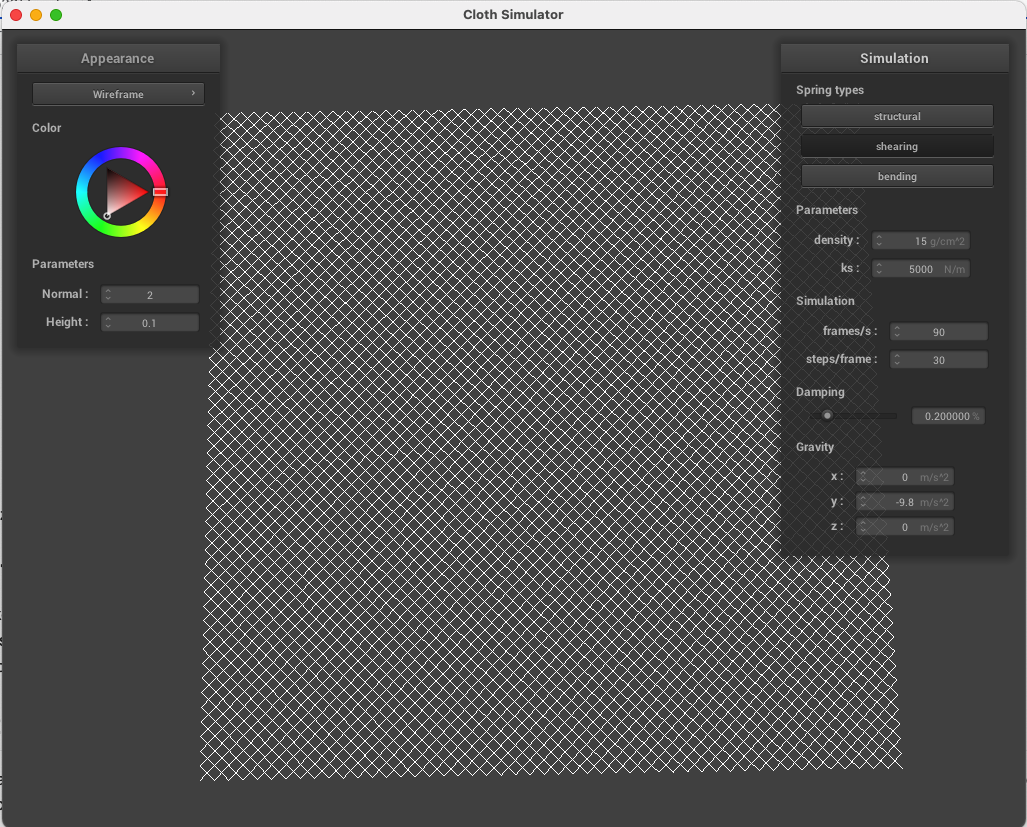
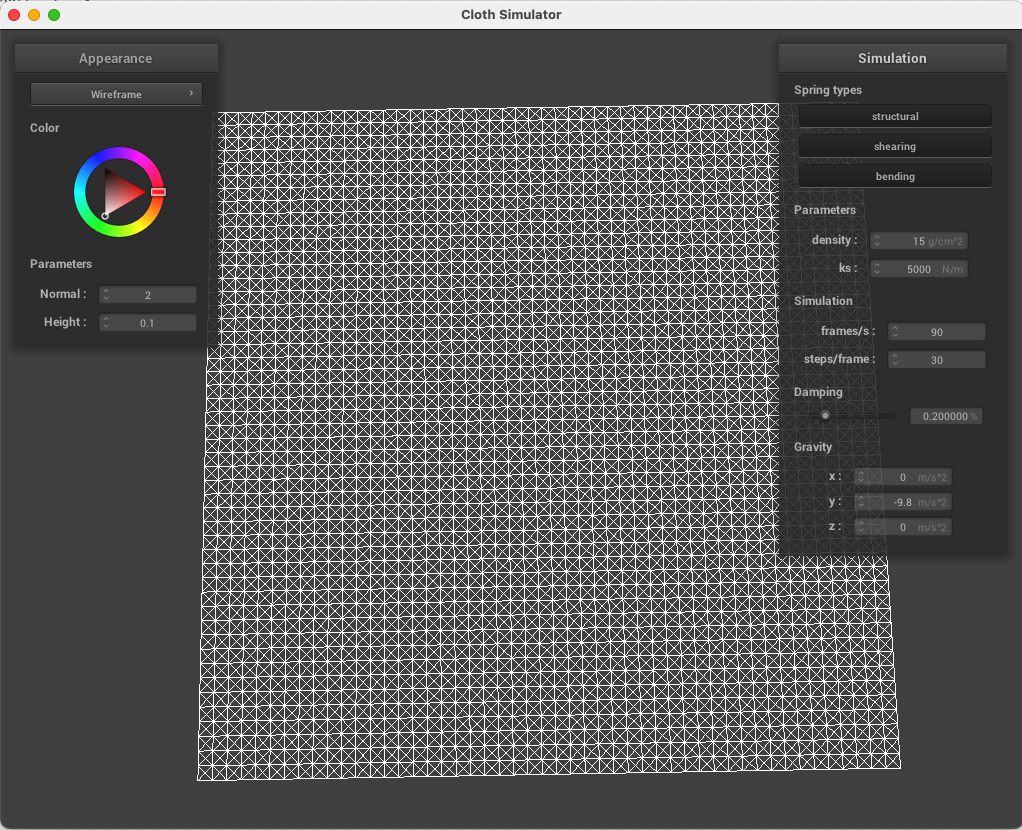
Below, the wireframe can be seen with no shearing constraints (only structure and bending), just shearing constraints, and then all three types of springs.
In this task, we used the spring force equations derived from the cloth structure as well as the Verlet integration method to simulate the evolution of the cloth over time. Because our simulation is flexible, we were able to see the result of changing various values.
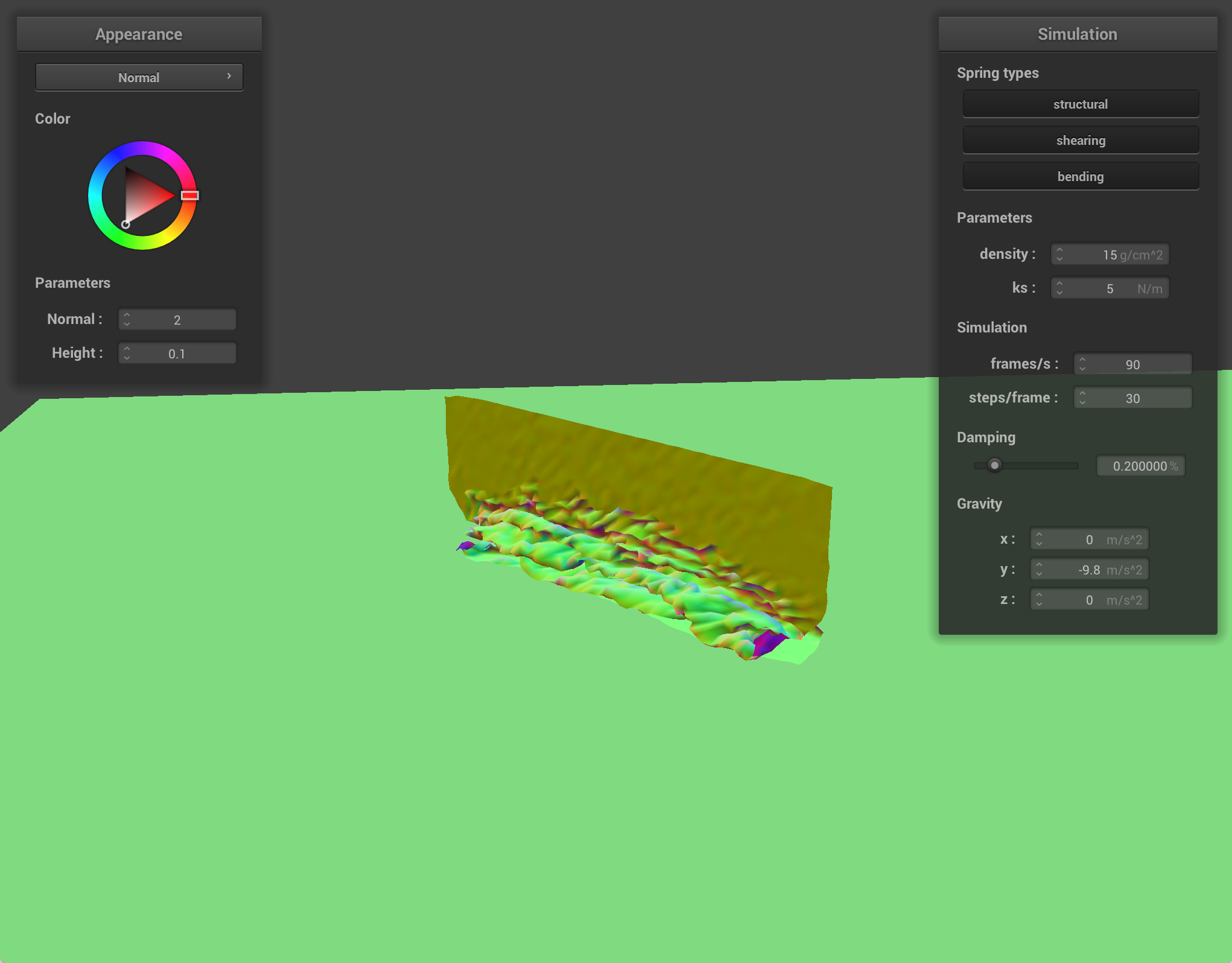
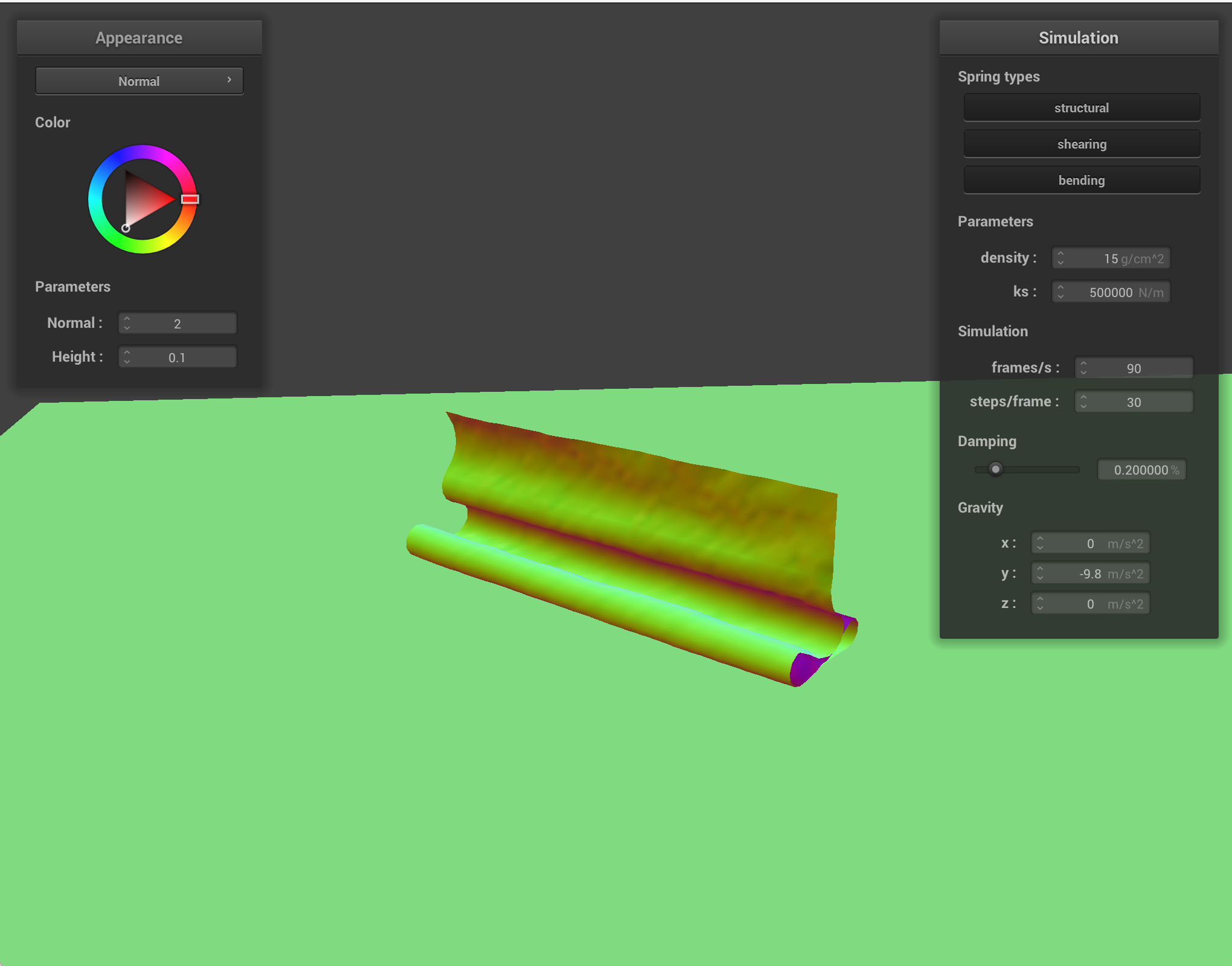
Spring constant: a higher spring constant could be seen to make the model very rigid, whereas a low spring constant led to the model jiggling around wildly. Below: default ks versus default / 1000, causing noticeable shimmering in the structure of the cloth.
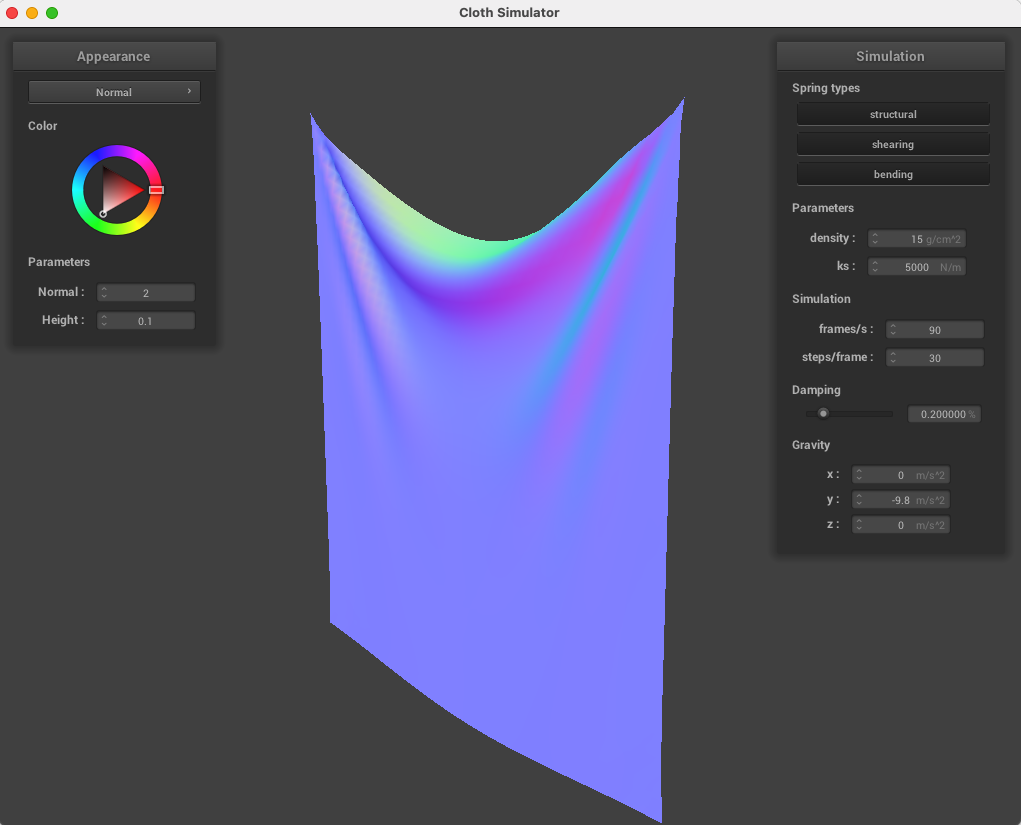
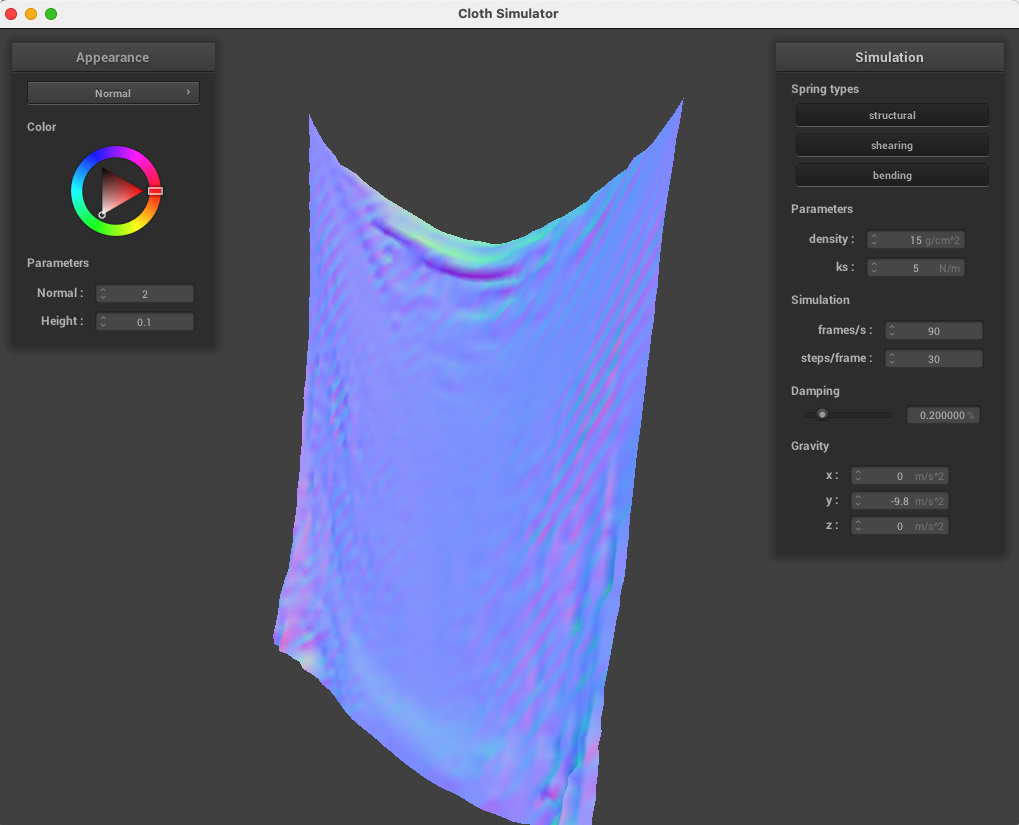
Density: the density of the material affects the result of all other forces, so a very high density leads to more pronounced spring forces and dramatic effects of gravity. A low density, then, resulted in much less perceived force on the cloth. Below: default density and density 1000 times the default, causing continuous motion due to much higher force.

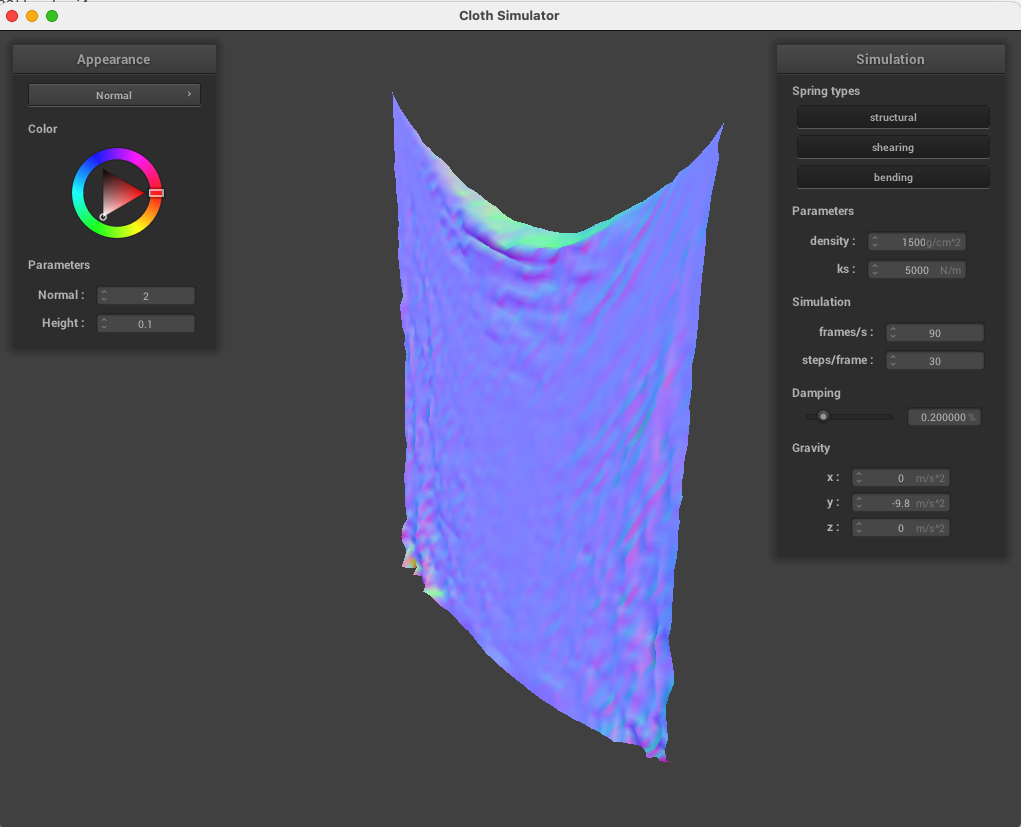
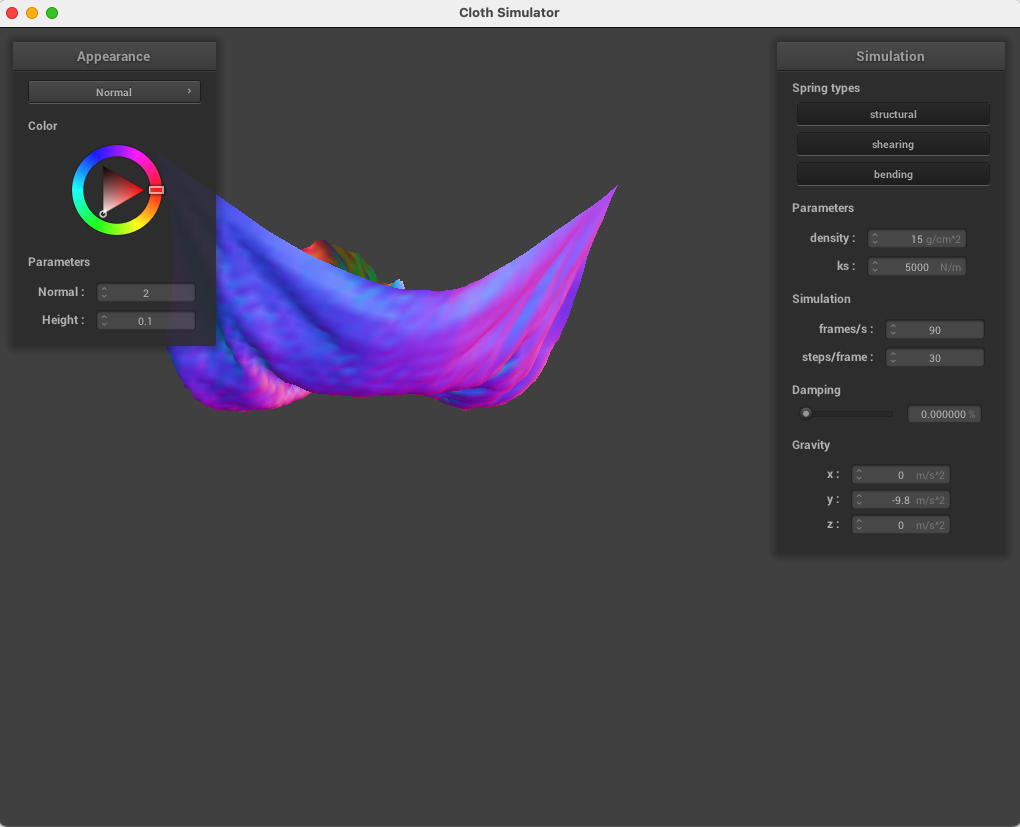
Damping: damping affects how much forces diminish over time, so with a very low damping, the cloth continues moving drastically for a long time, but a high damping causes the cloth to come to rest quickly. Below: default damping of 20% versus damping of 0%, causing the cloth to swing backward quickly.

Below is the resting state of the cloth given the default parameters.
In this task, we created methods to handle colliding the cloth and its constituent springs with spherical and planar objects.
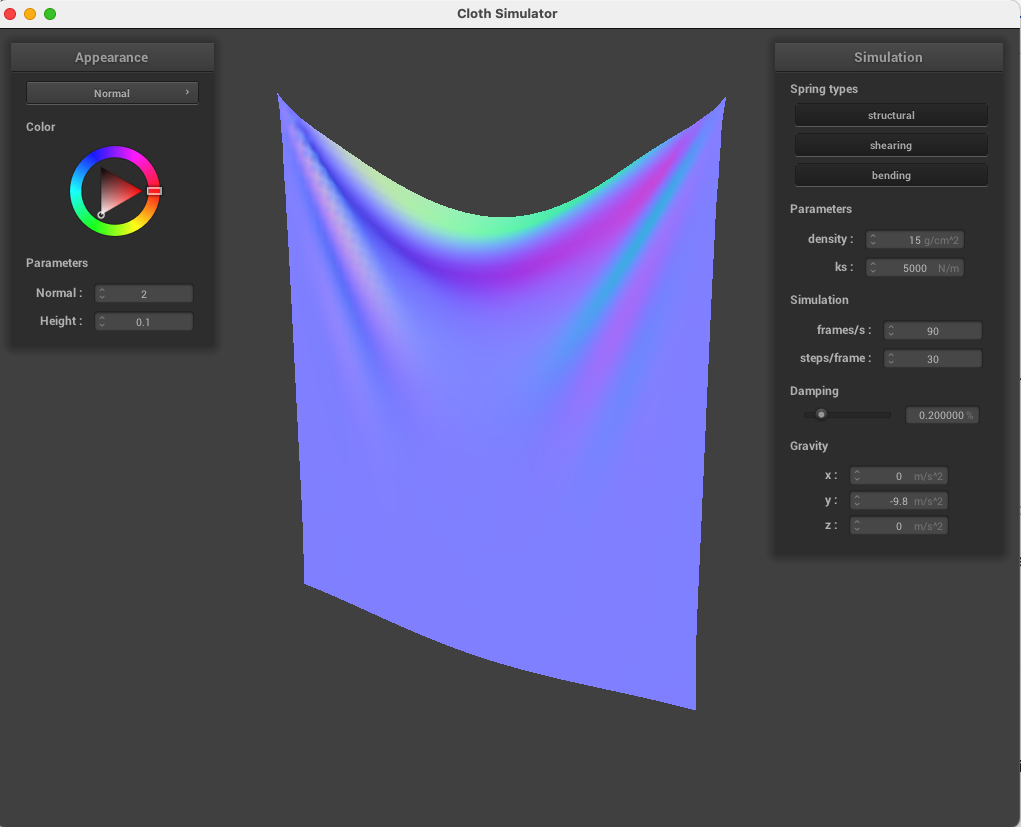
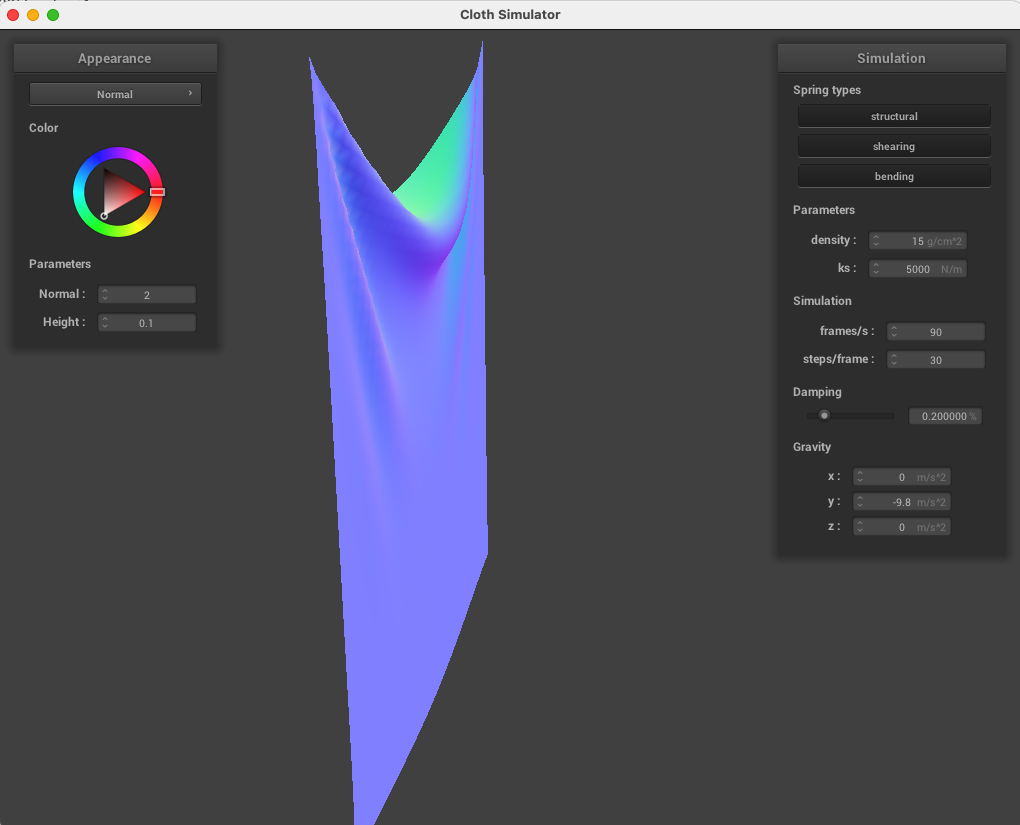
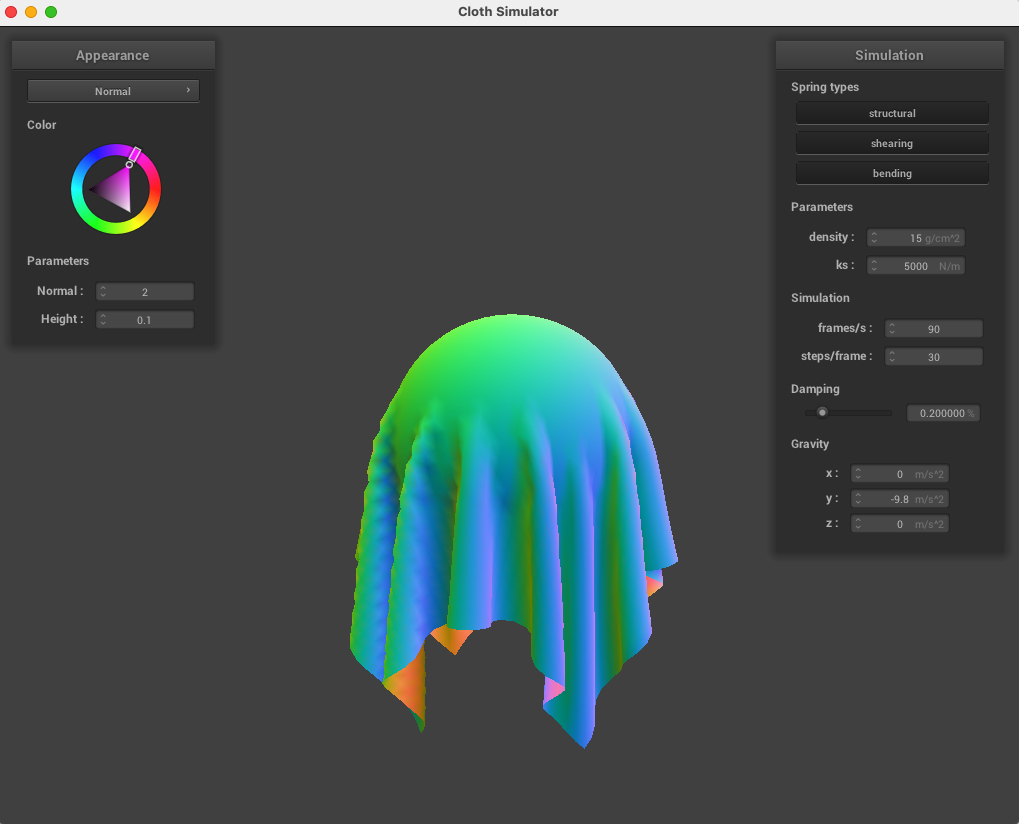
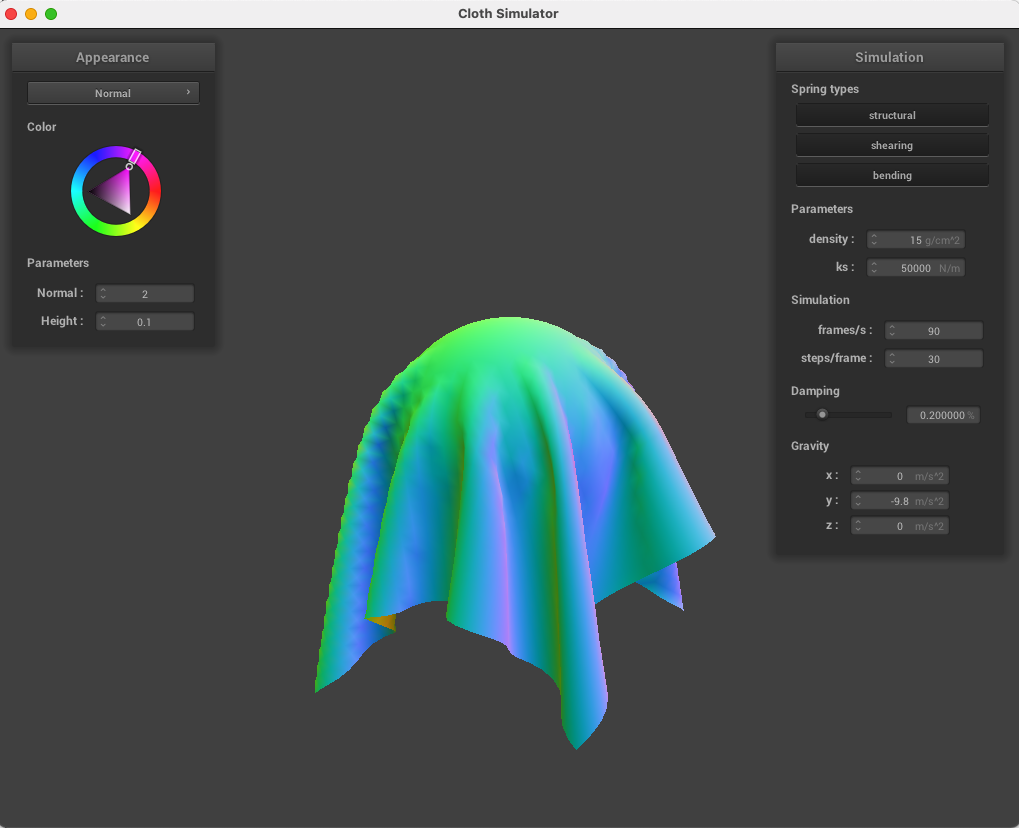
Below, we collided our cloth with sphere using spring coefficients of ks = 500, 5,000, and 50,000. Noticeably, the higher spring coefficients cause the material to rest farther from just due to the effects of gravity, with ks = 50,000 resulting in pronounced angles in between the edges of the cloth and the sphere.

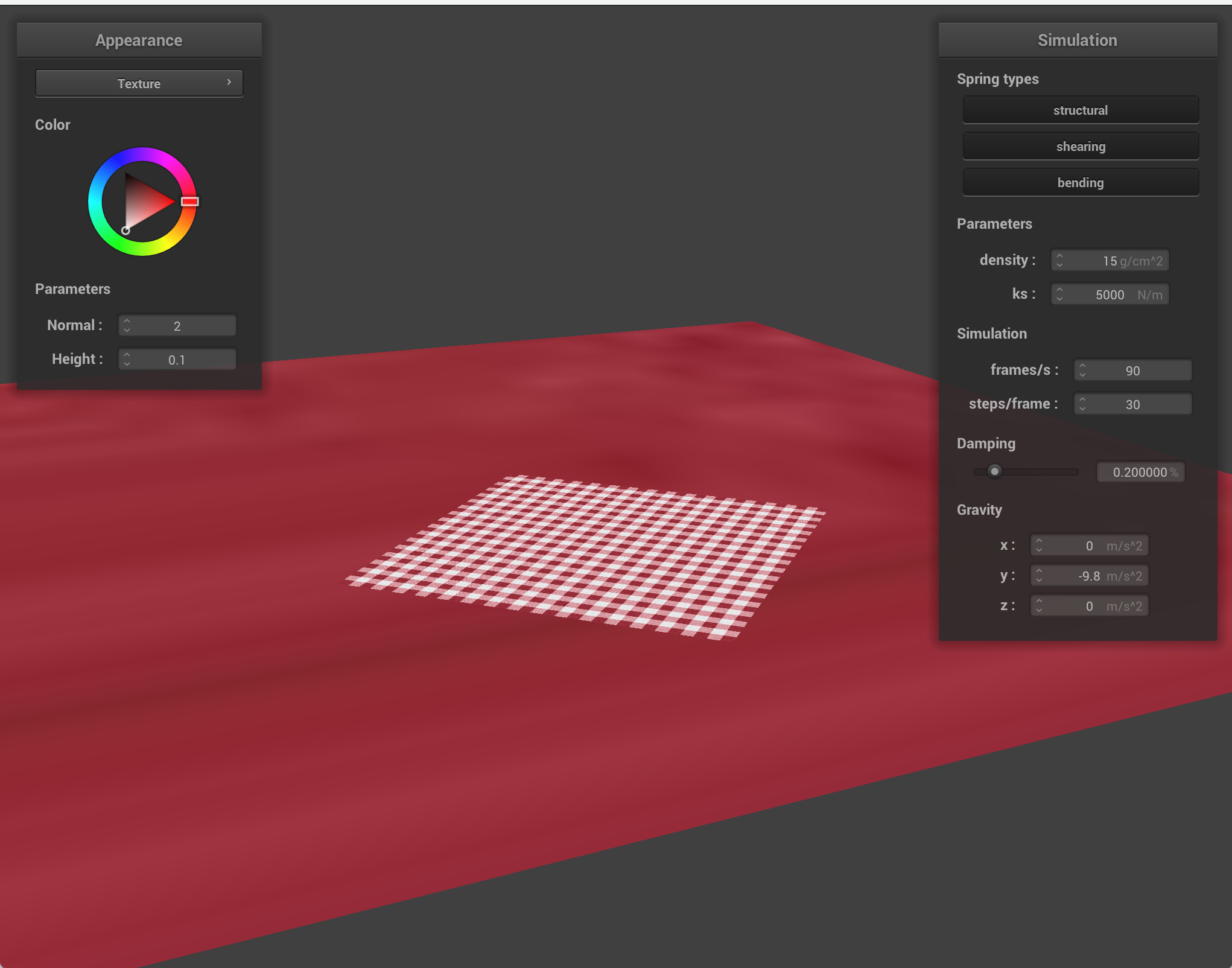
Below is our cloth colliding with a plane from above, textured with a picnic table and checkerboard texture.
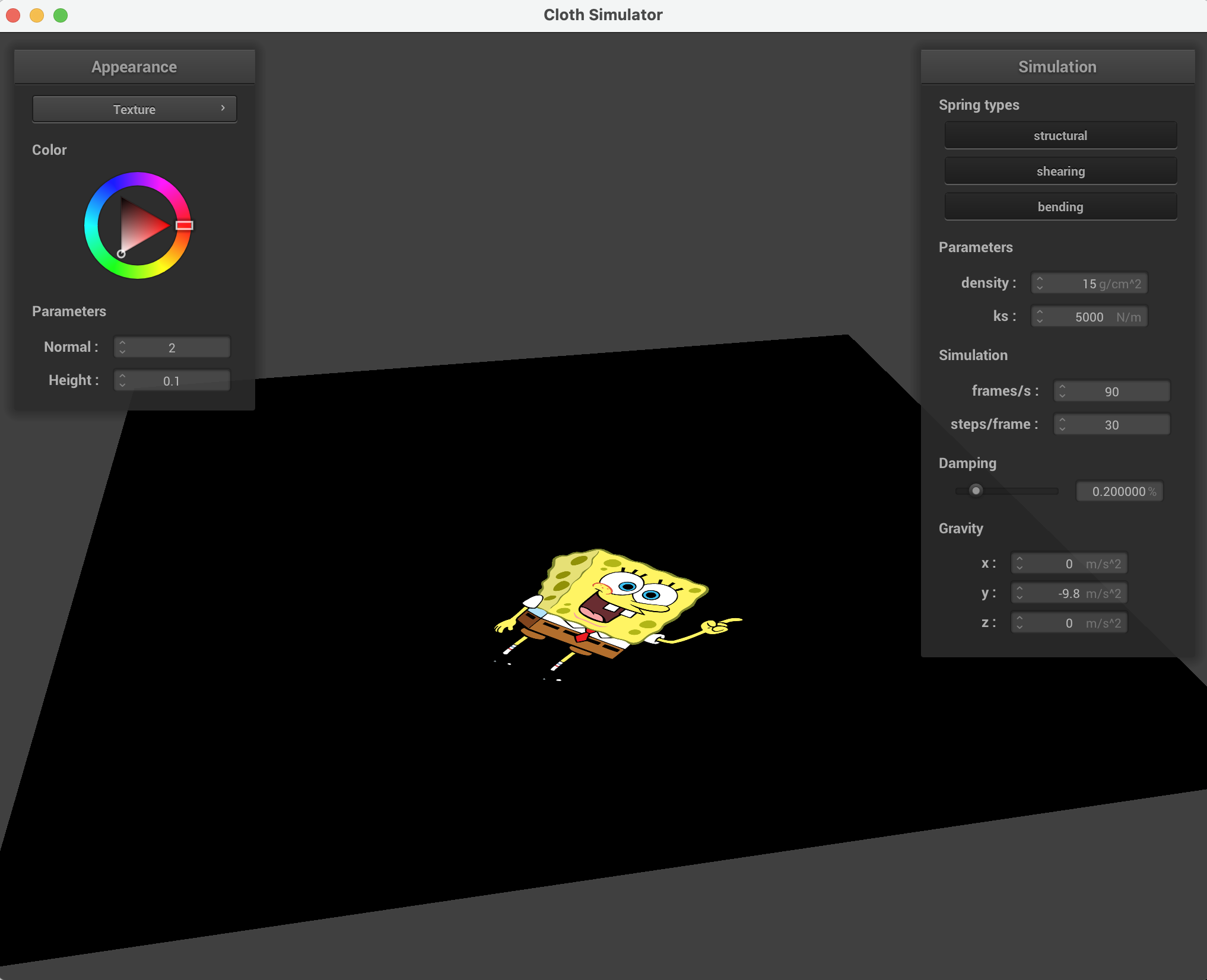
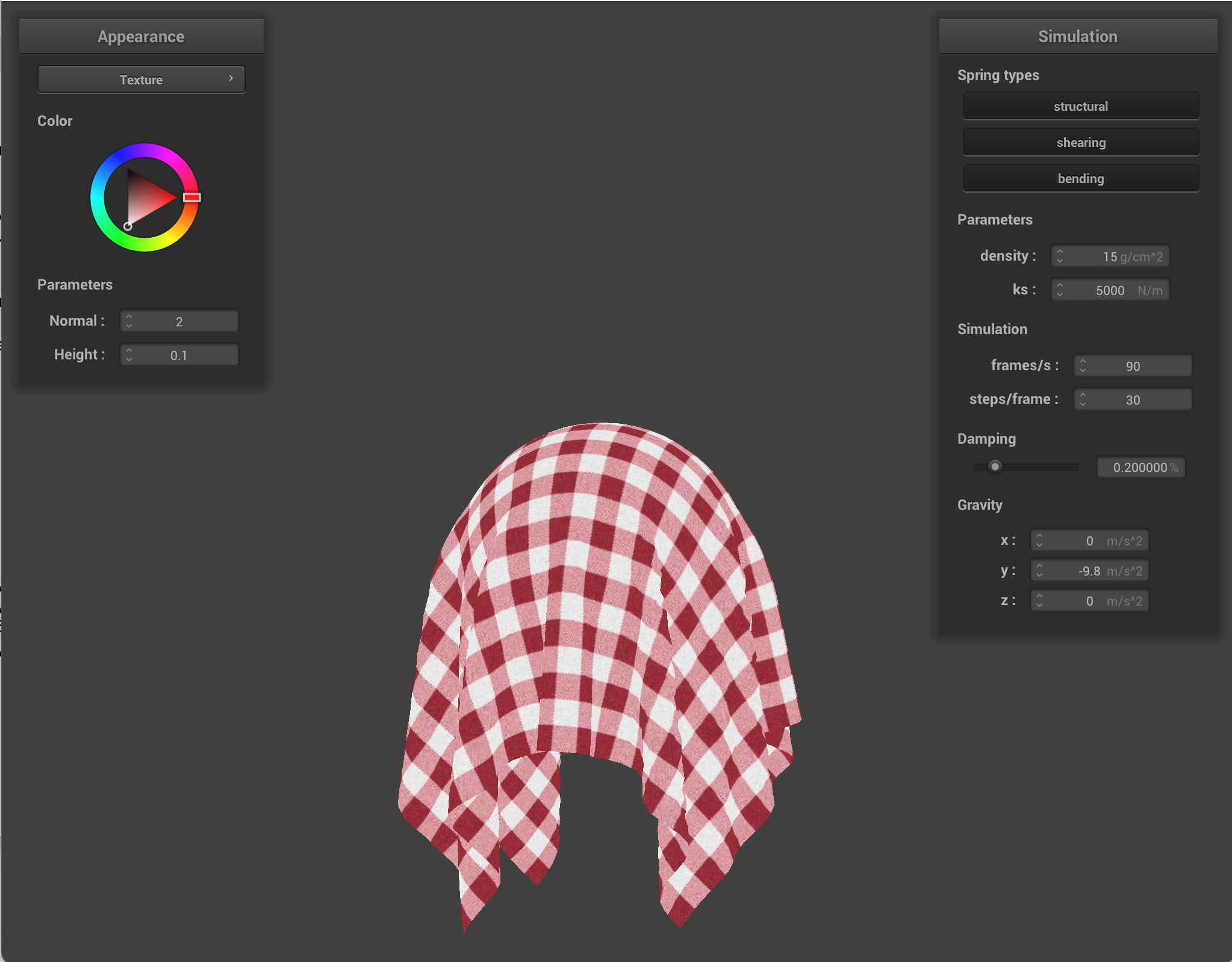
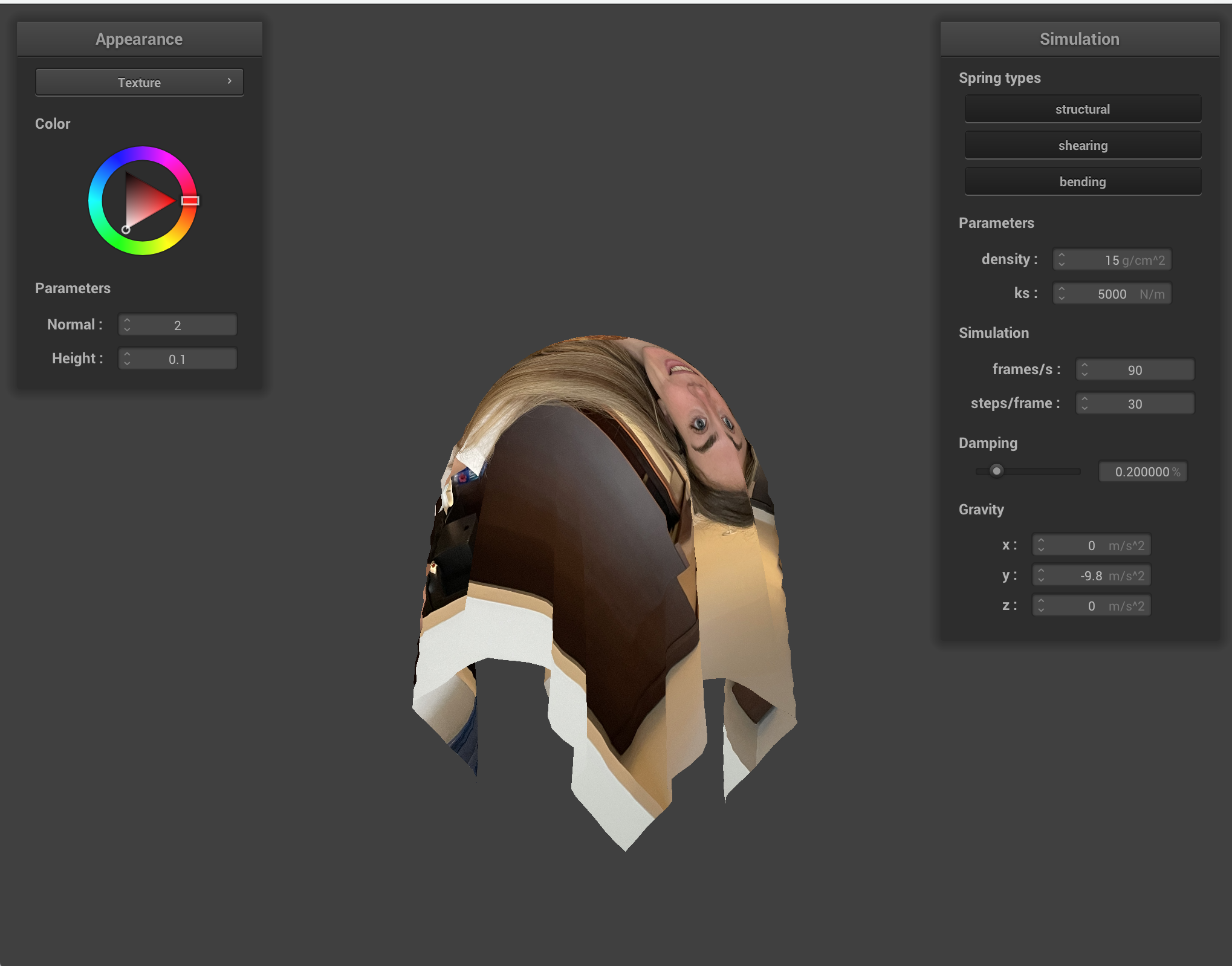
Below is our cloth colliding with a sphere from above, textured with a picnic table texture and an image of Sam's partner, Catherine, holding a baguette.
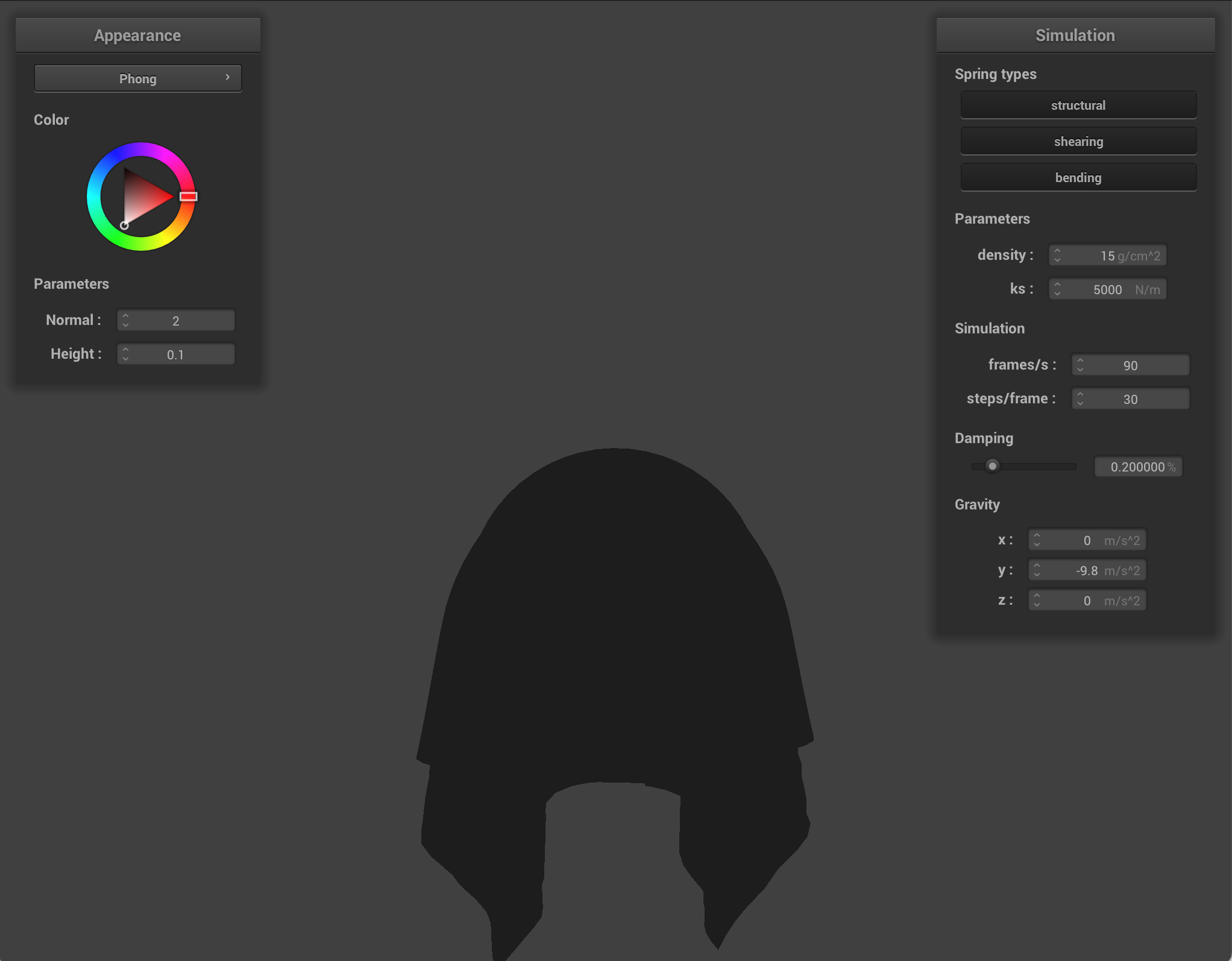
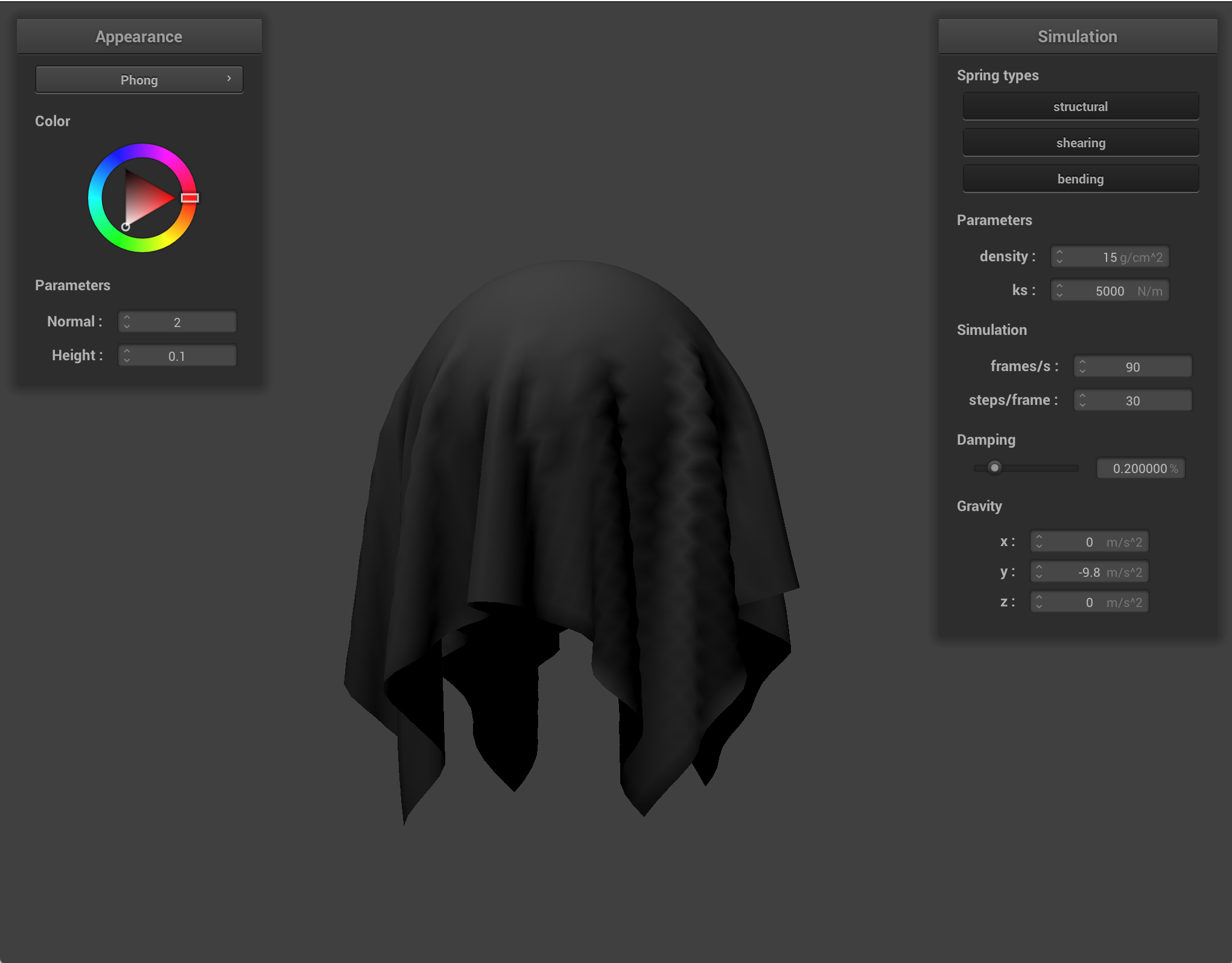
In this task, we implemented logic so that the cloth wouldn't collide with itself ("clipping"), but would instead realistically fold on itself in response to forces. Below are six screenshots of the cloth falling (with normal shading). The cloth first begins to fold at the bottom, then as it has almost entirely hit the ground, it starts to really fold over itself, ending up completely folded in half.
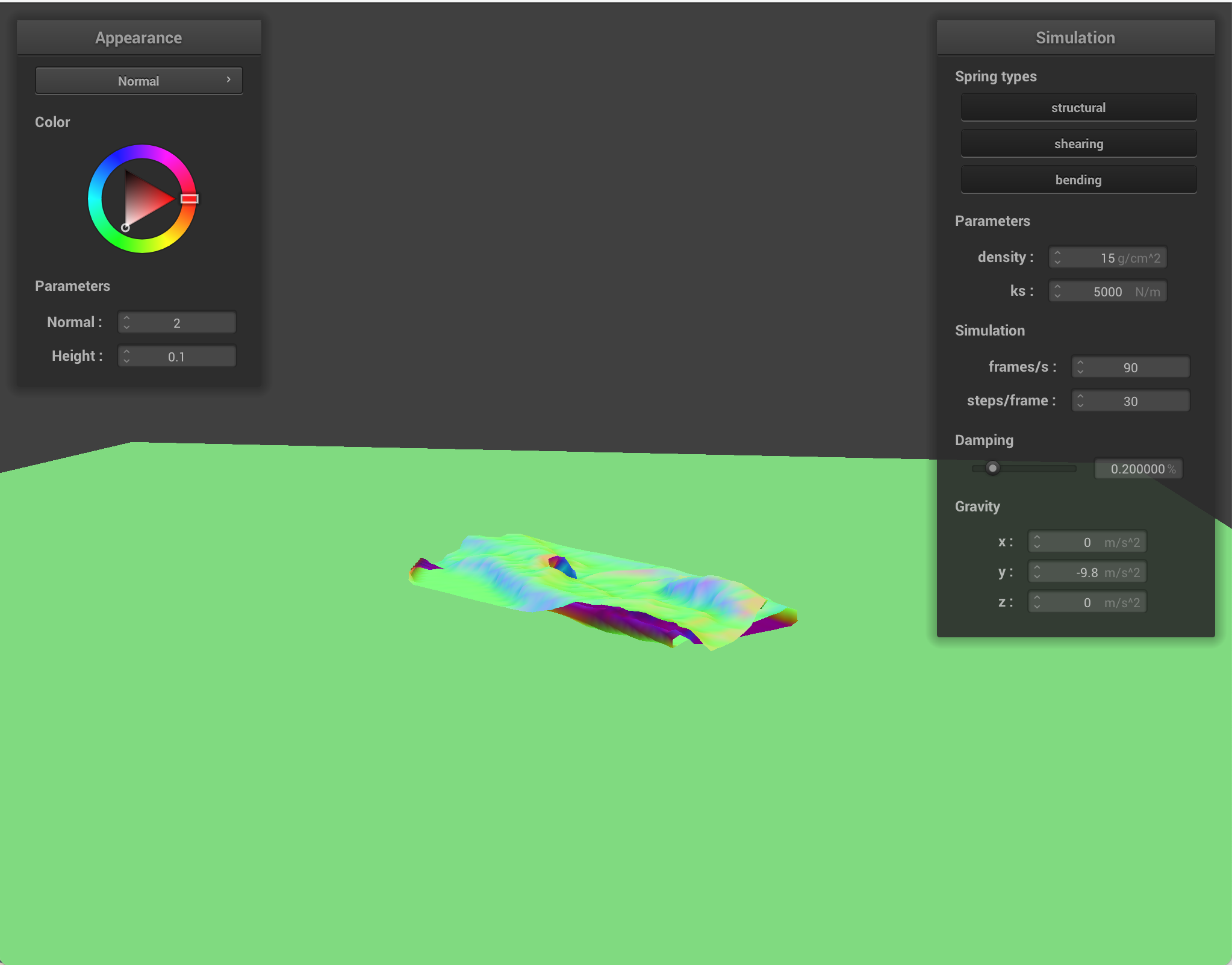
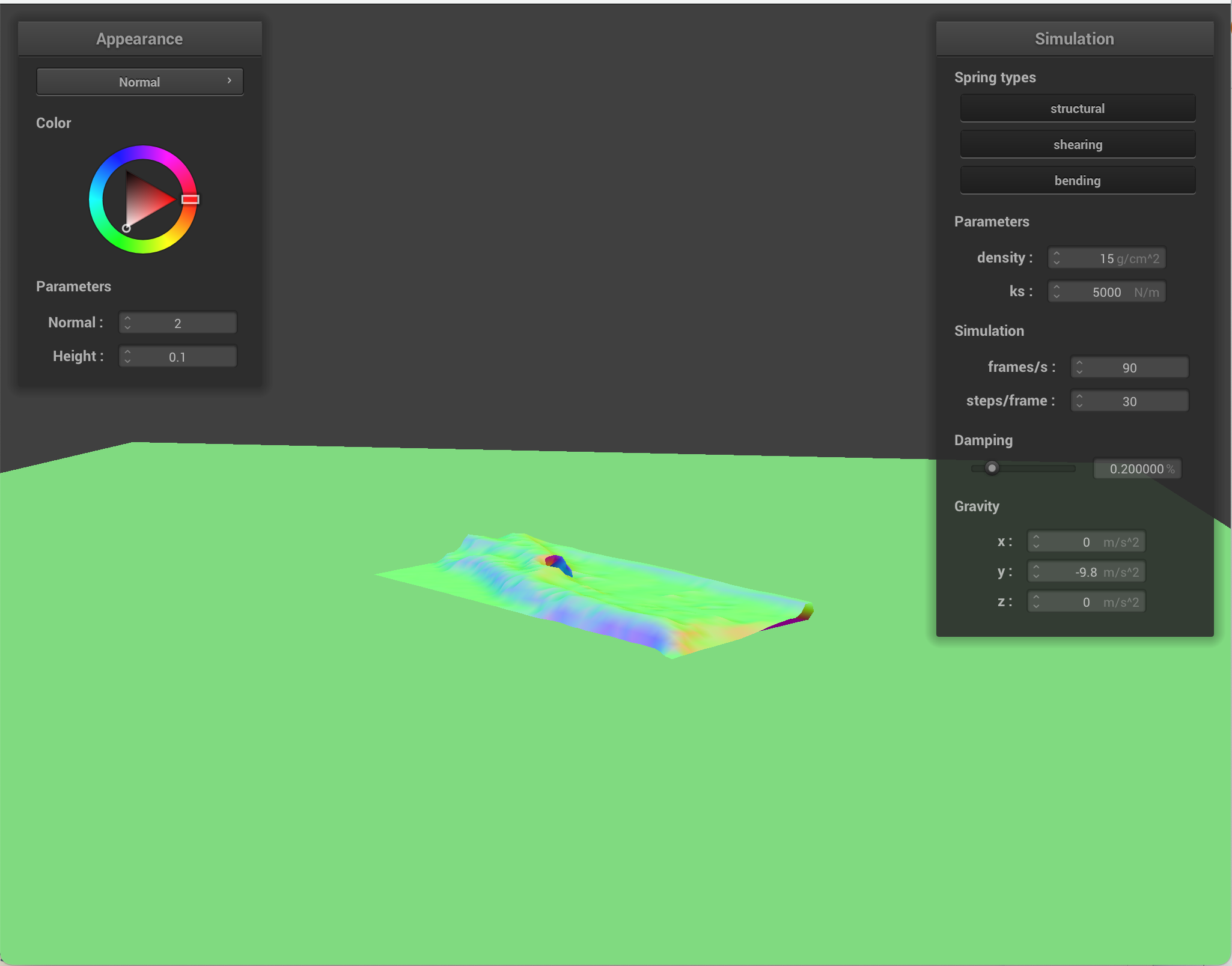
Density: as before, higher density caused a stronger force on the cloth, resulting in bounciness, whereas low density caused the cloth to come to a stop earlier. Below: regular density vs. 100x density, causing the cloth on the right to fall faster.
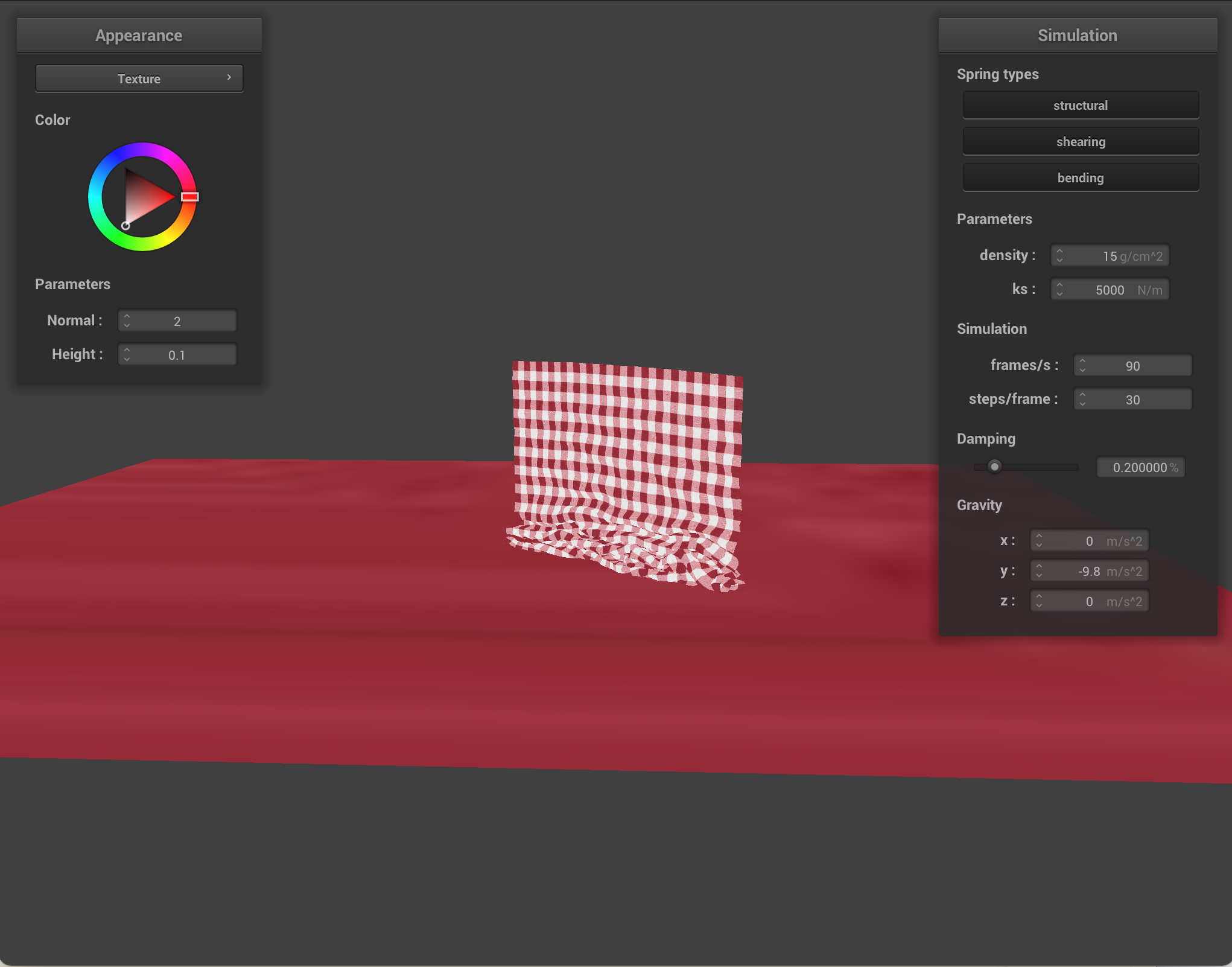
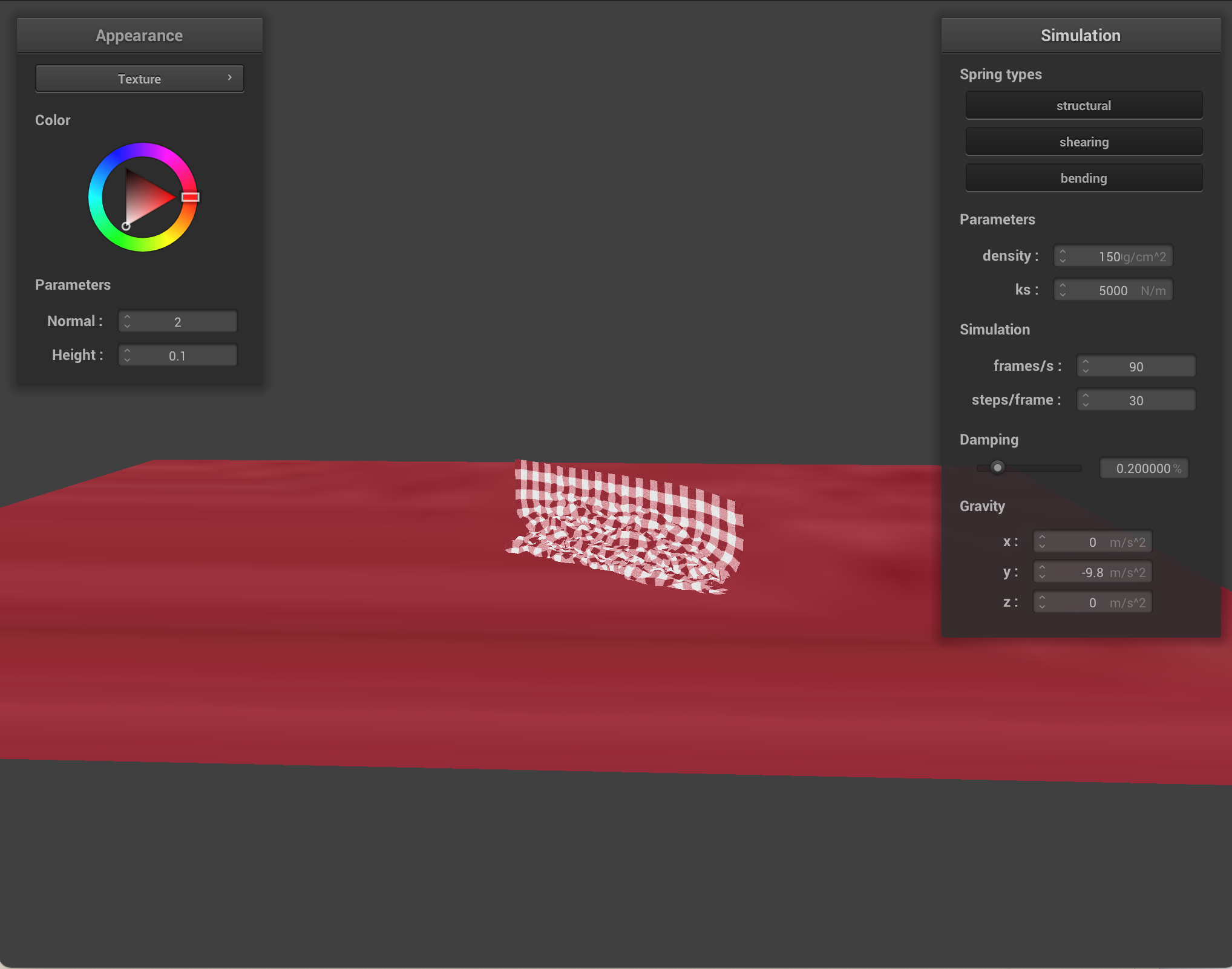
Spring constant: a high spring constant led to very rigid movement (structural and other constraint springs not bending as far in response to the same force), whereas very low spring constant led to the cloth bouncing around wildly. Below, the left shows a cloth with ks = 1/1000 times the default, and the right shows a cloth with ks = 1000 times the default.
In this task, we used GLSL to implement a variety of methods of shading objects. For this, we used .vert and .frag files. .vert files allowed us to generalize and parallelize operations over all vertices, and then the outputs of these .vert files were used as inputs to .frag files, which used the values relevant to each vertex and a given procedure to calculate the color at that point.
One of the main shaders, Blinn-Phong, is a clever combination of three kinds of lighting: diffuse, ambient, and specular that approximates real world reflection, global illumination, and shine effectively. Below, the sphere and cloth are shown with just the ambient component, just the diffuse component, just the specular component, and then the whole Blinn-Phong model.
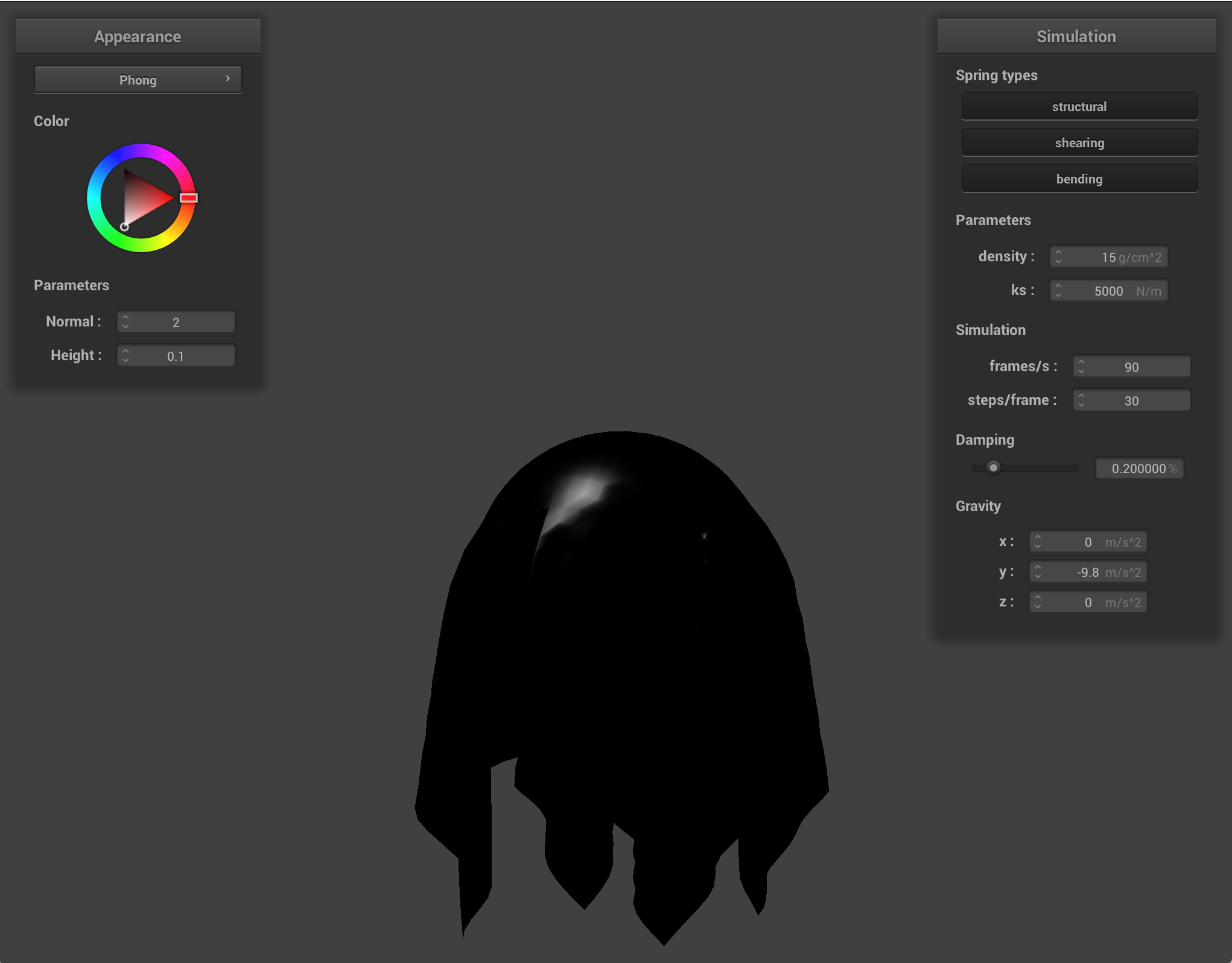
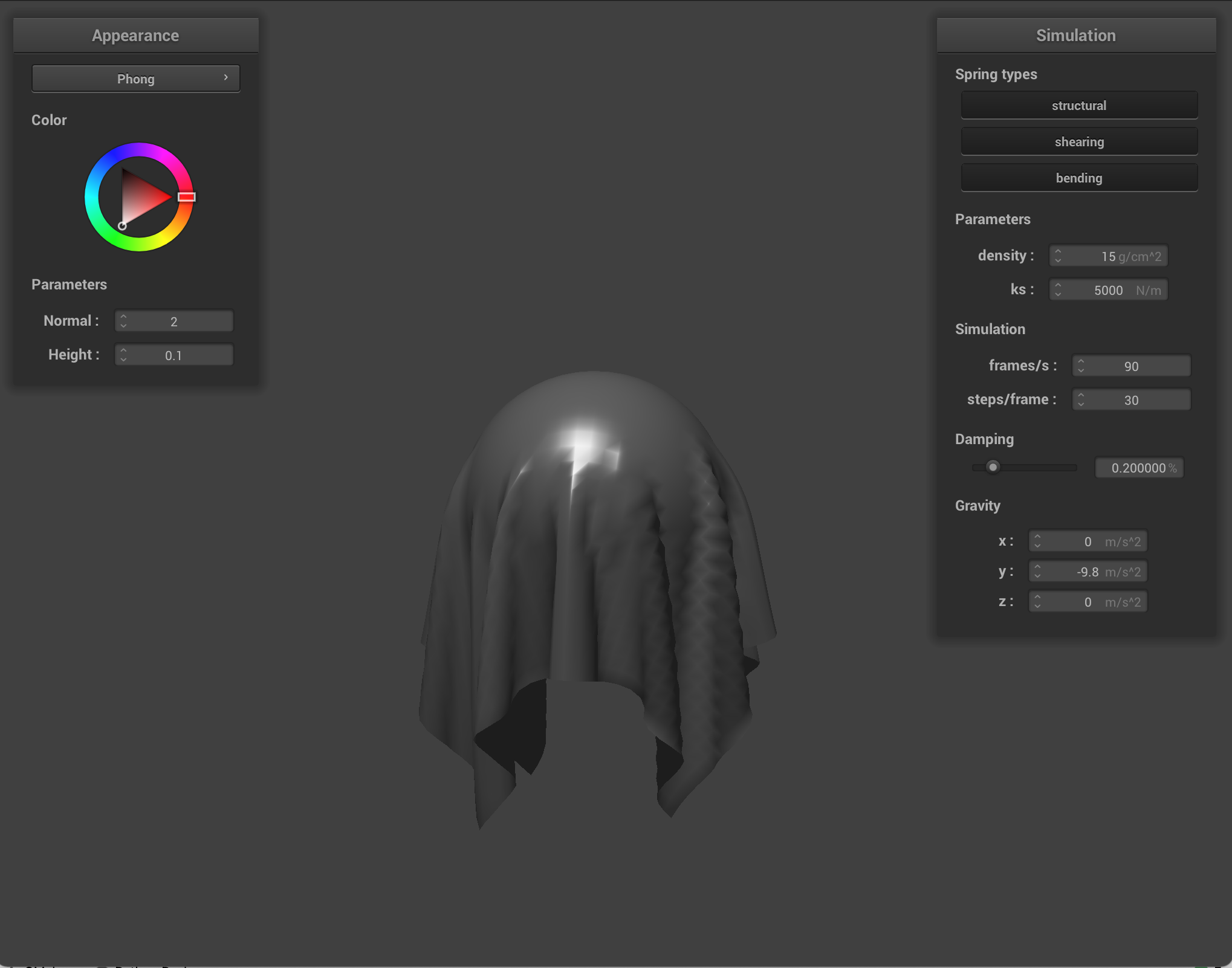
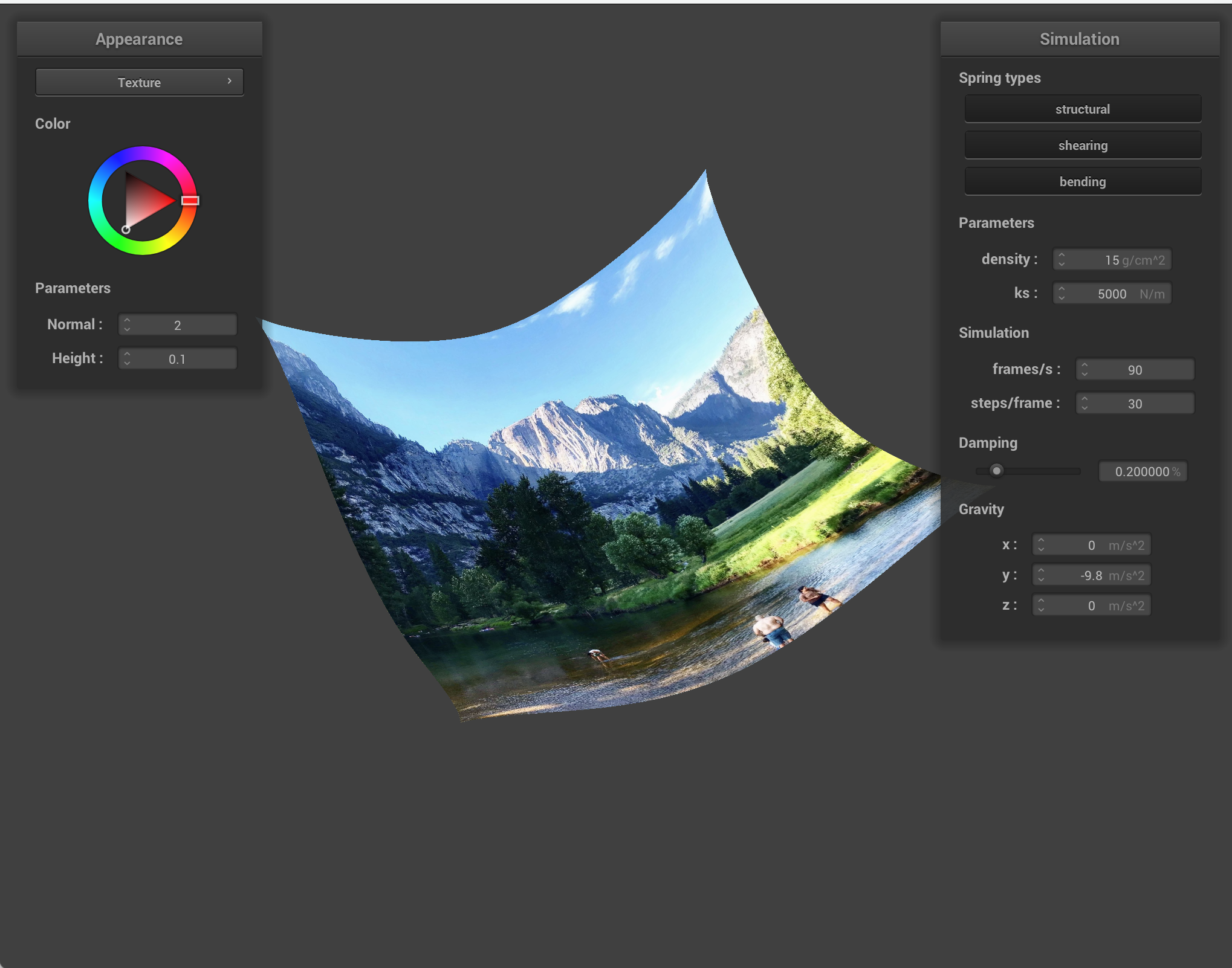
Another shader type we introduced was the ability to map shaders onto our objects, so below is Sam's partner Catherine holding a baguette mapped onto a falling cloth and a photo of Yosemite mapped onto another cloth.

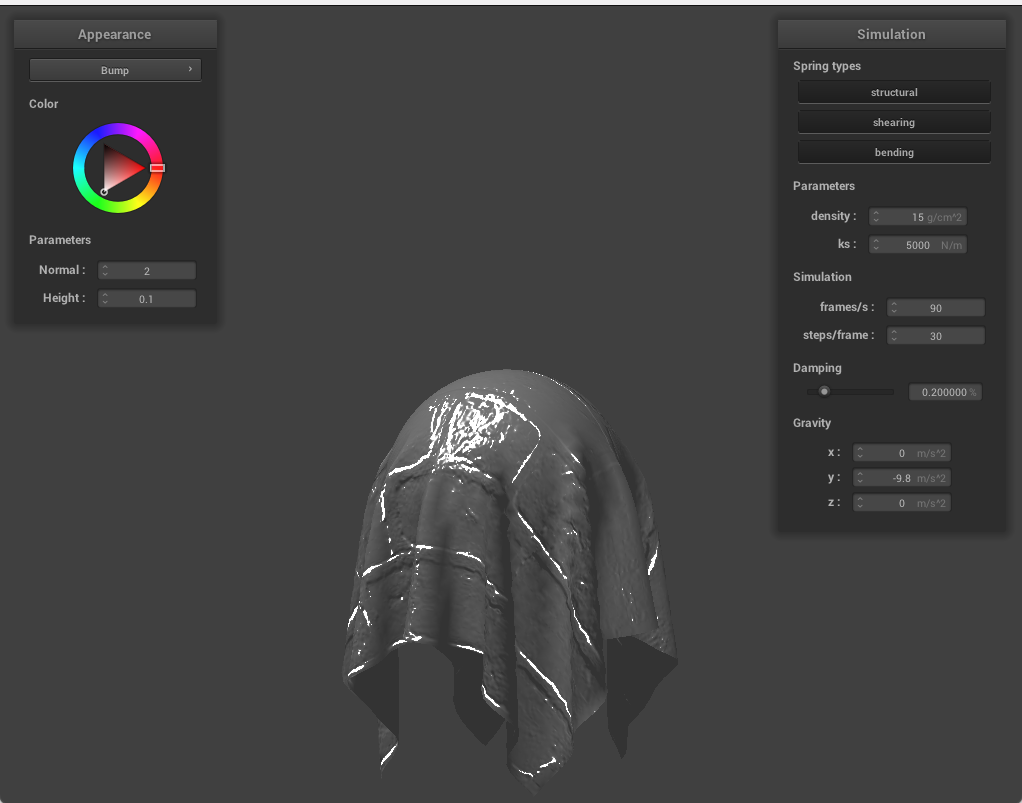
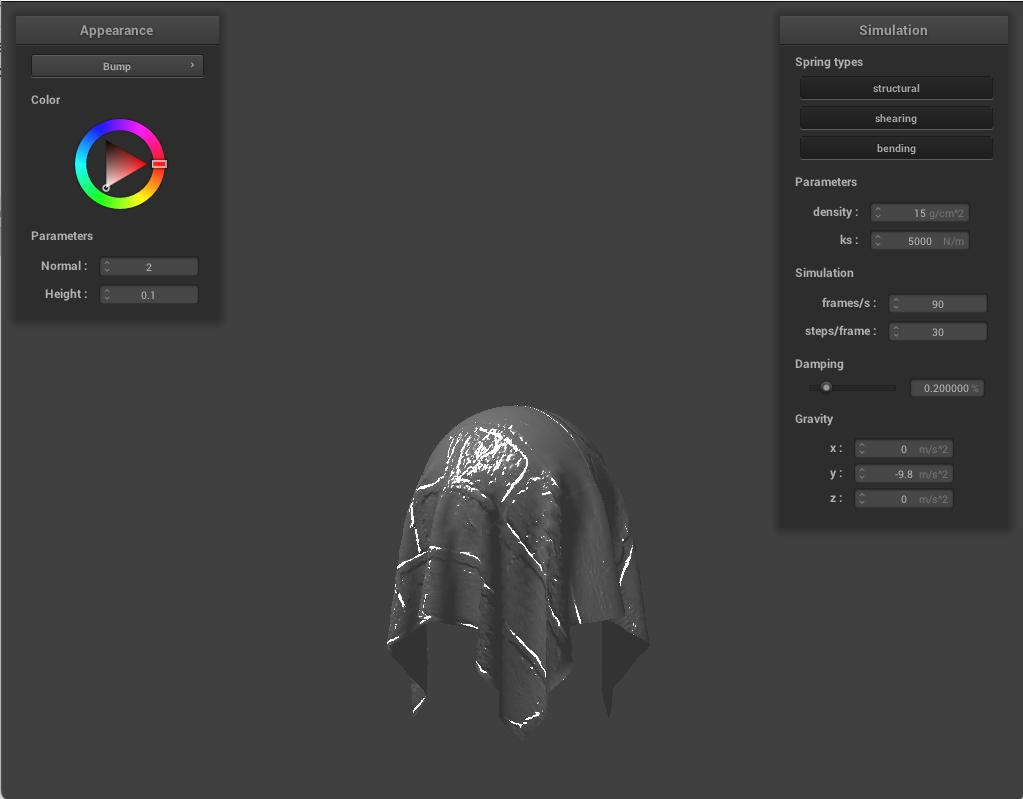
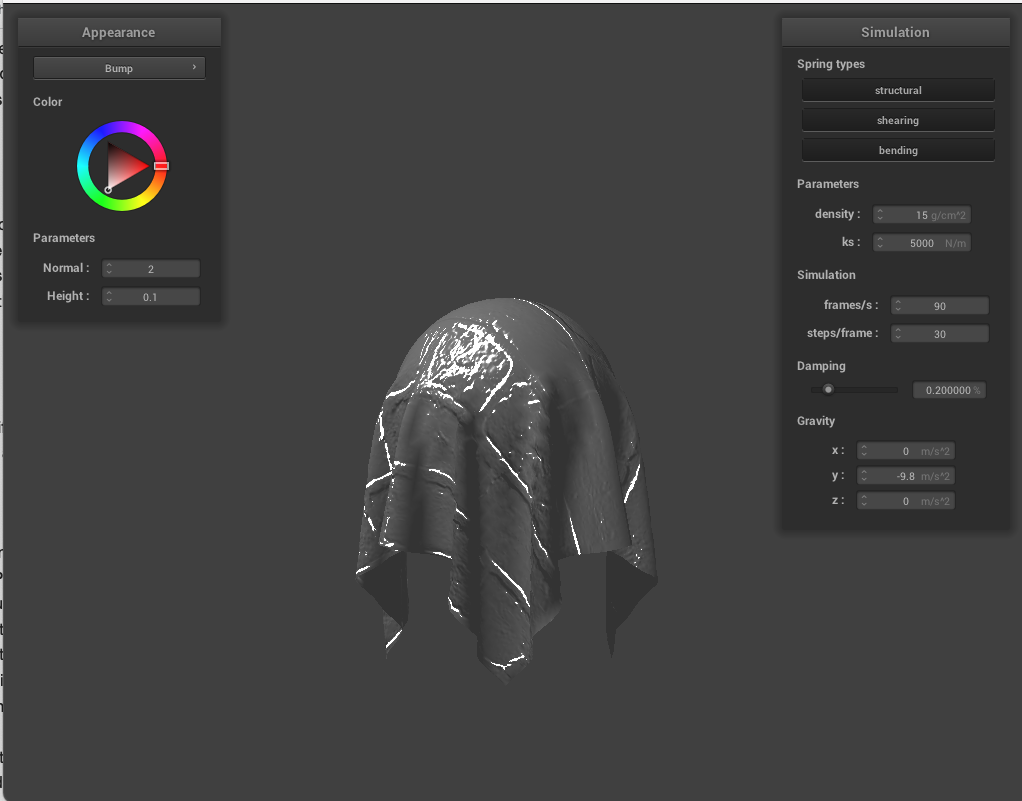
Below, we showcase our bump shading (exterior changes) and displacement shading (physical changes to the points on the materials) using texture_3, which looks like bricks. Both textures have noticeable shading features due to the layout of the bricks, but the displacement shading seems much more 3 dimensional, with the mortar between the bricks being visible.
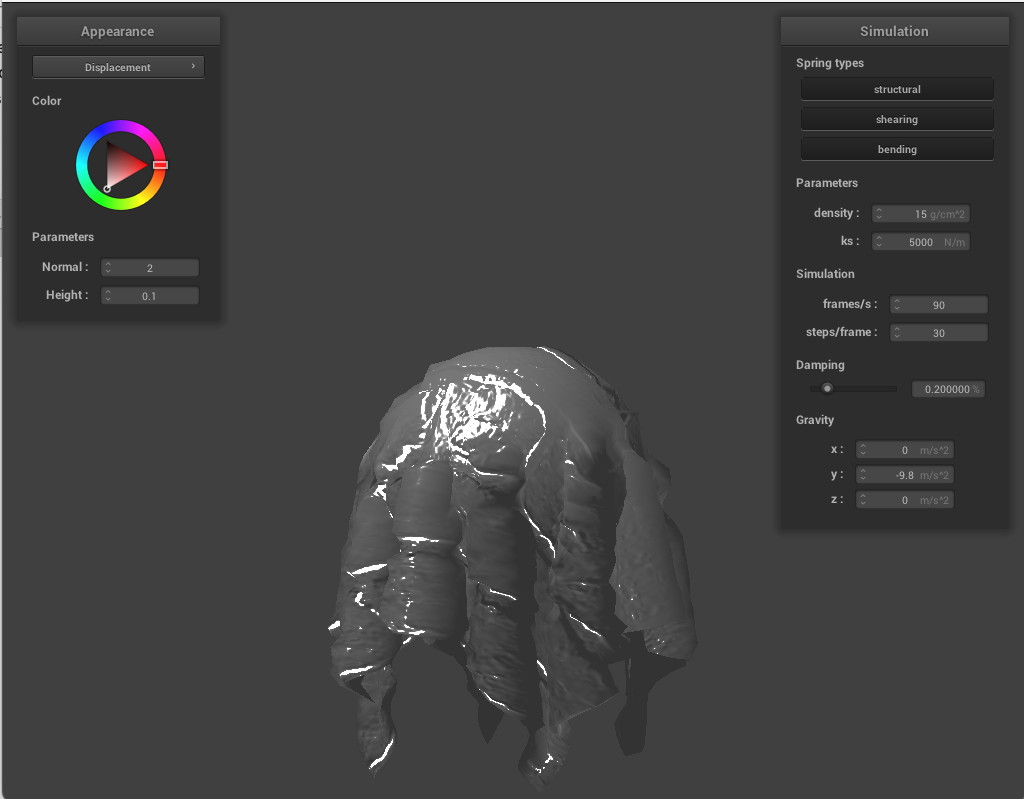
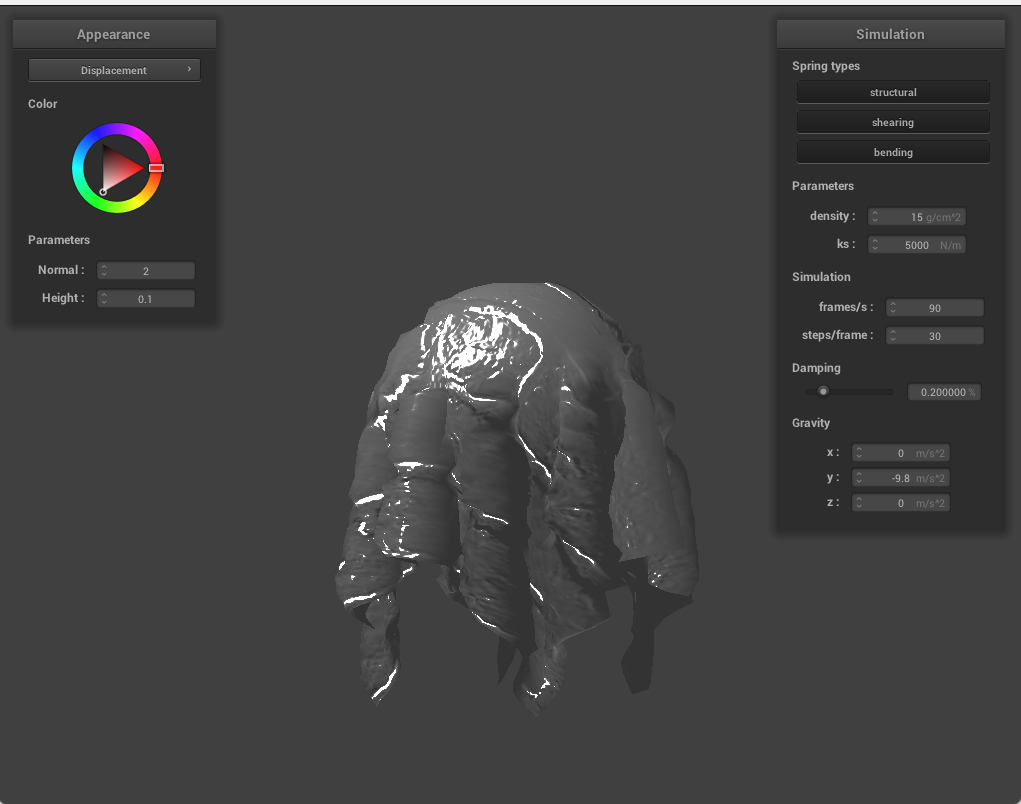
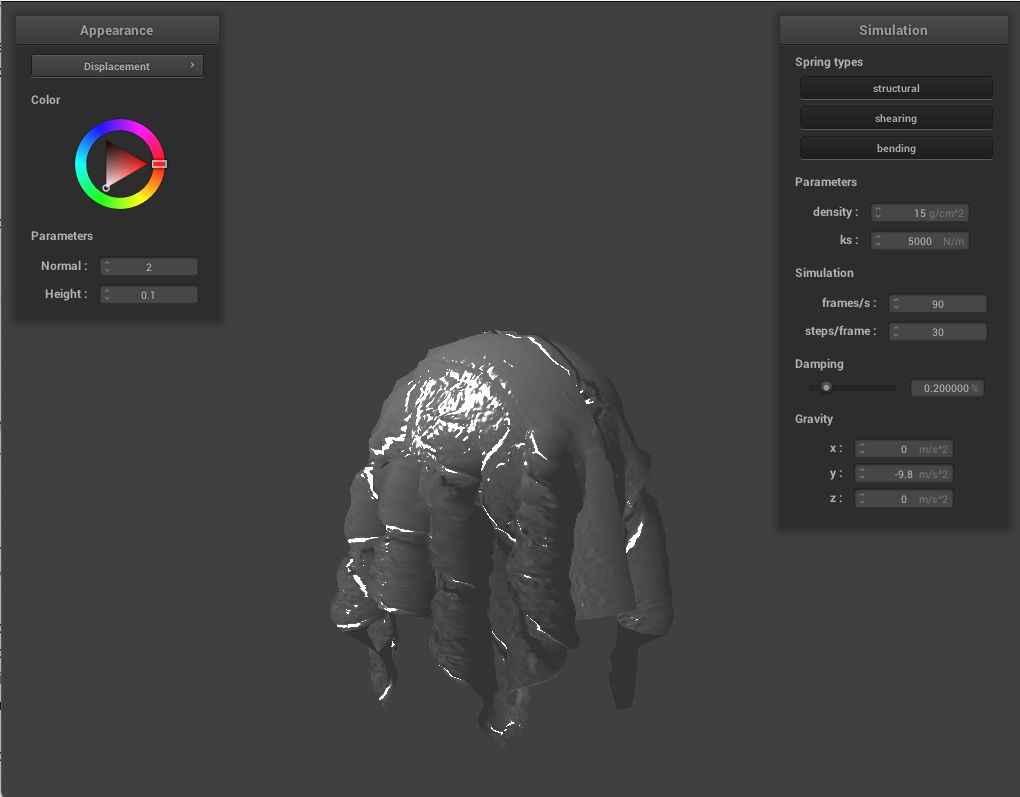
Below, we use the same shaders but change the sphere's coarseness. On the top left is less coarse sphere with displacement shading, and on the top right with a more coarse sphere. The bottom row are the same for bump shading. Noticeably, for displacement shading, the more coarse sphere has smoother geometry to land on, where for the bump shading, this difference is purely cosmetic.
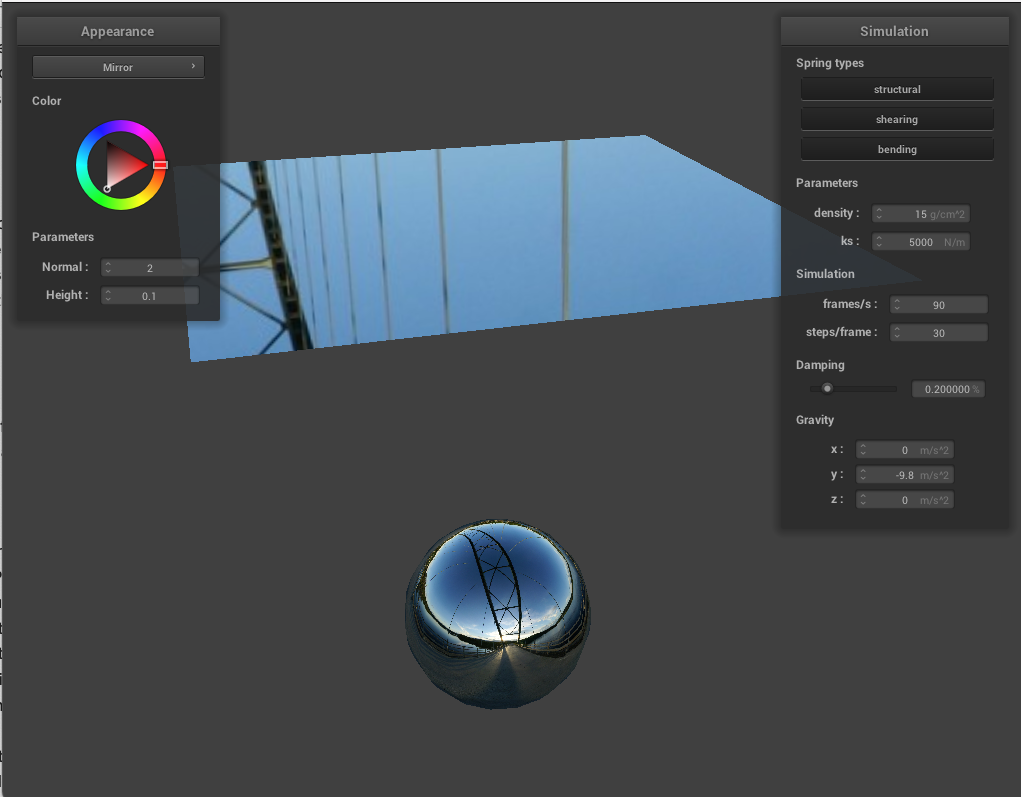
Finally, below is the sphere shown with an environnment mapping that mirrors a lovely cube texture.
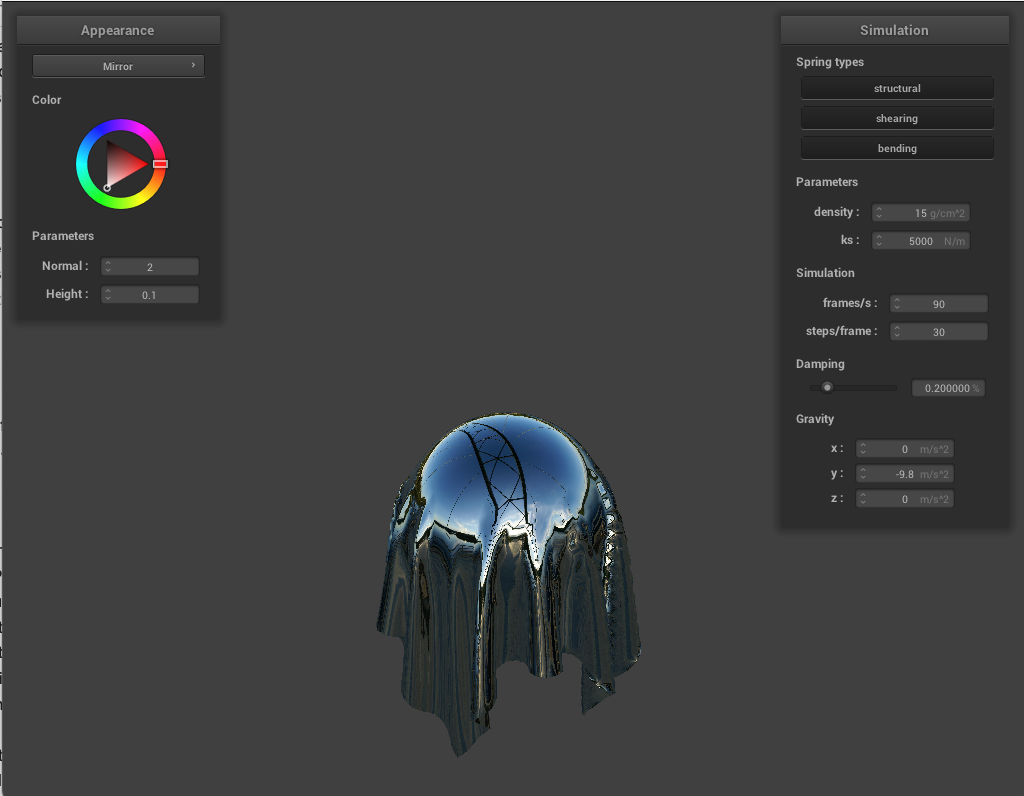
Using physics simulation has been really rewarding - all of the key graphical knowledge that we've built up so far (rasterization, meshes, shading, and collision) are able to come together in order to produce realistic progression through time. We will continue this kind of simulation for our final project.
Hosted at https://cal-cs184-student.github.io/sp22-project-webpages-nimarez/proj4/index