CS 184: Spring 2022
Sam Ellgass and Nima Rezaeian
In this project, we implemented Bezier surfaces with de Casteljau subdivision, halfEdgeMesh operations, and the Loop Subdivision algorithm to upsample triangle meshes. It was especially informative to see how the halfEdgemesh data structure made traversal, assignment, and other operations both convenient and generalizable! The upsampling of meshes is an incredibly powerful tool - being able to turn the low resolution meshes into high resolution polygons in seconds with just a few functions was very rewarding.
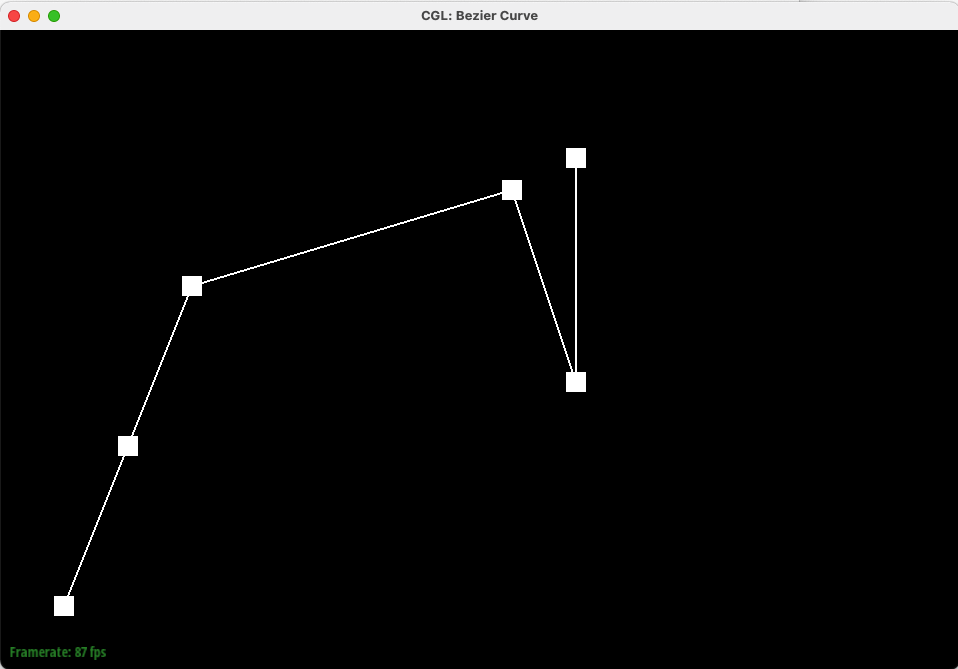
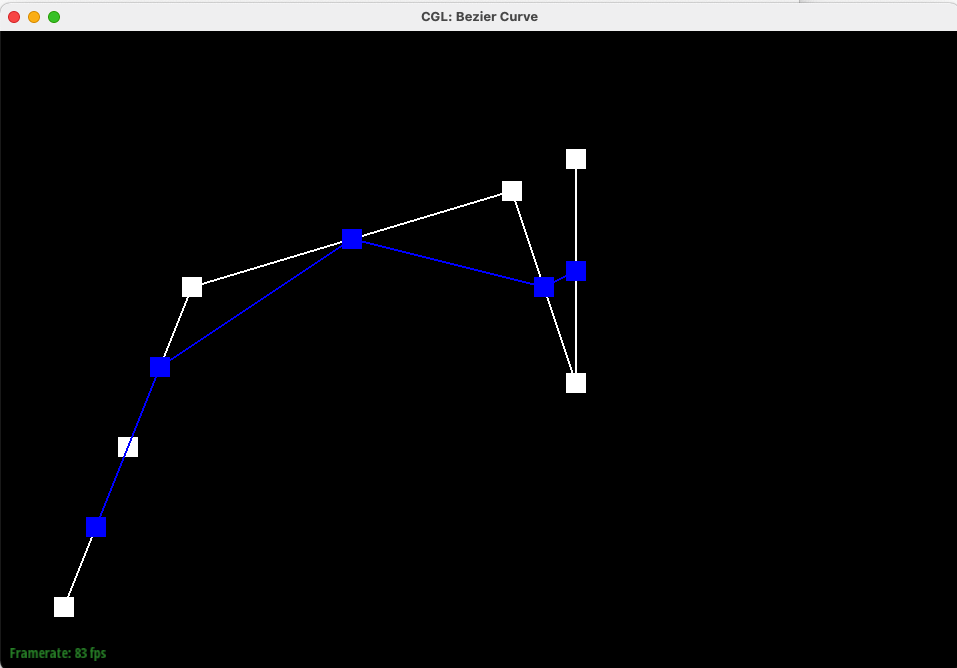
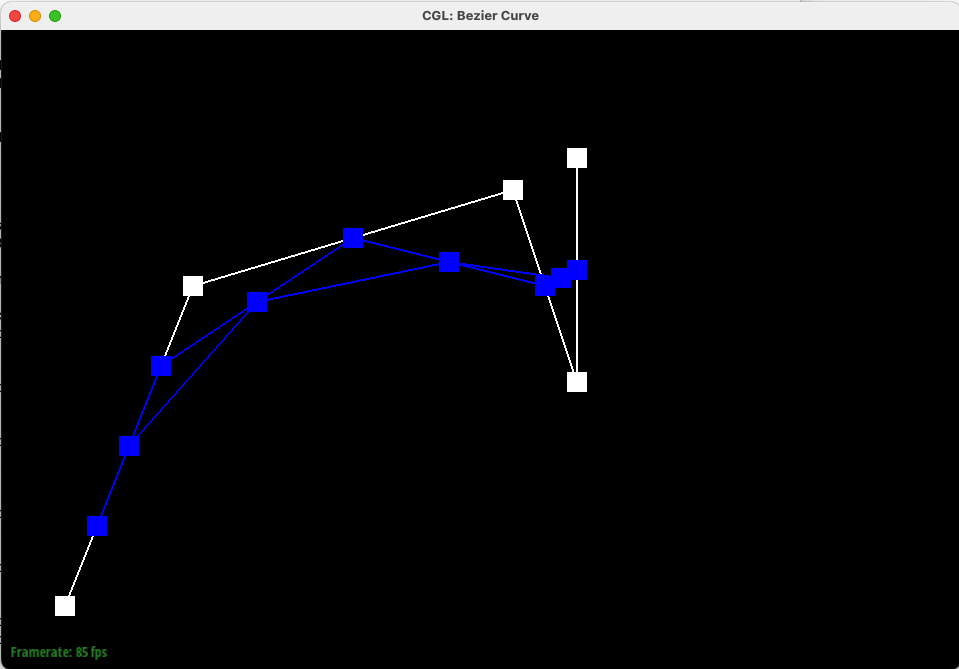
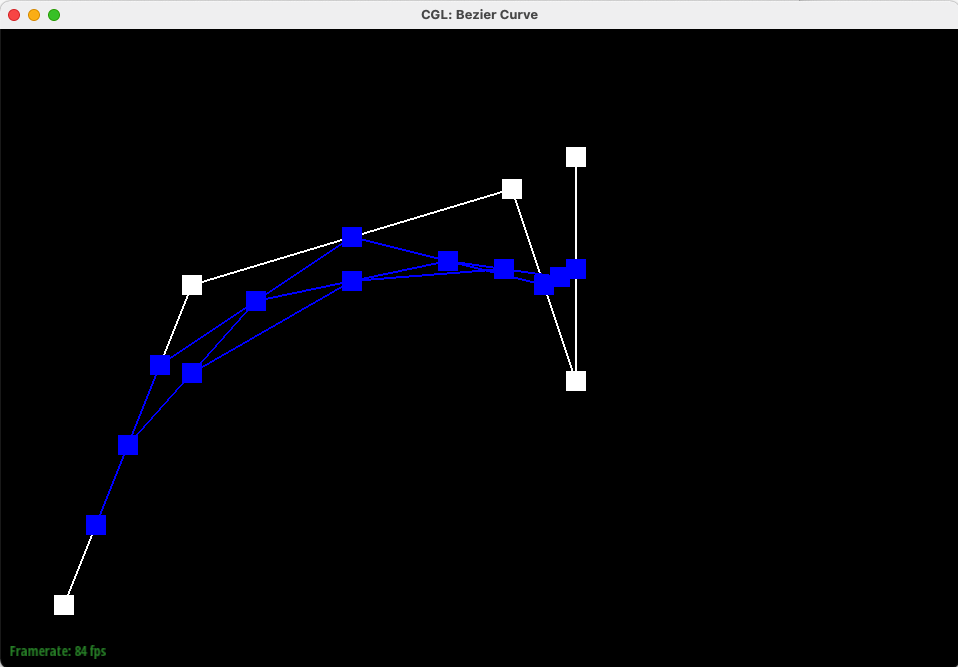
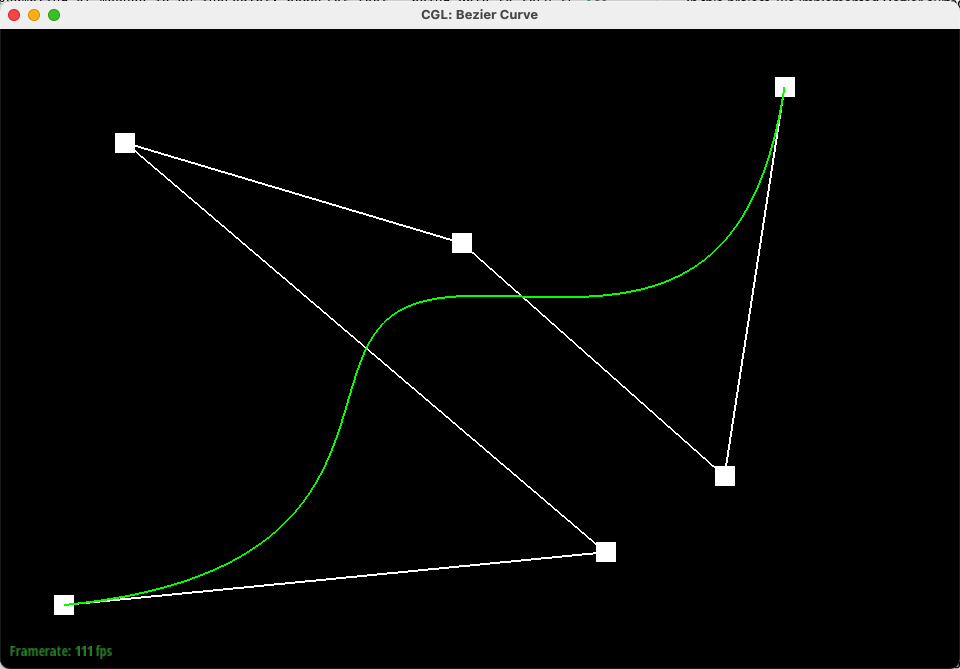
In this task, we implemented Bezier Curves with 1D de Casteljau subdivision. De Casteljau's algorithm leverages repeated linear interpolation to create a smooth curve from given control points. These N control points (splines) can be moved around as the starting points of N-1 iterations of linear interpolation to create the Bezier Curves.
Below is our Bezier curve with 6 control points, starting from level 0 (no interpolation) iteratively to level 5 (a single interpolated point on the Bezier Curve).



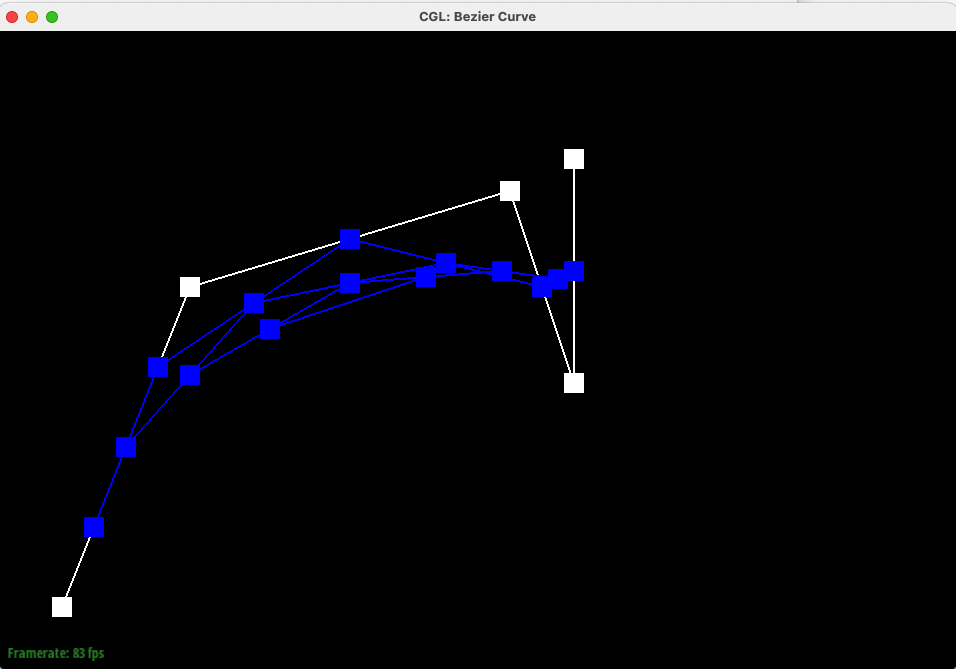
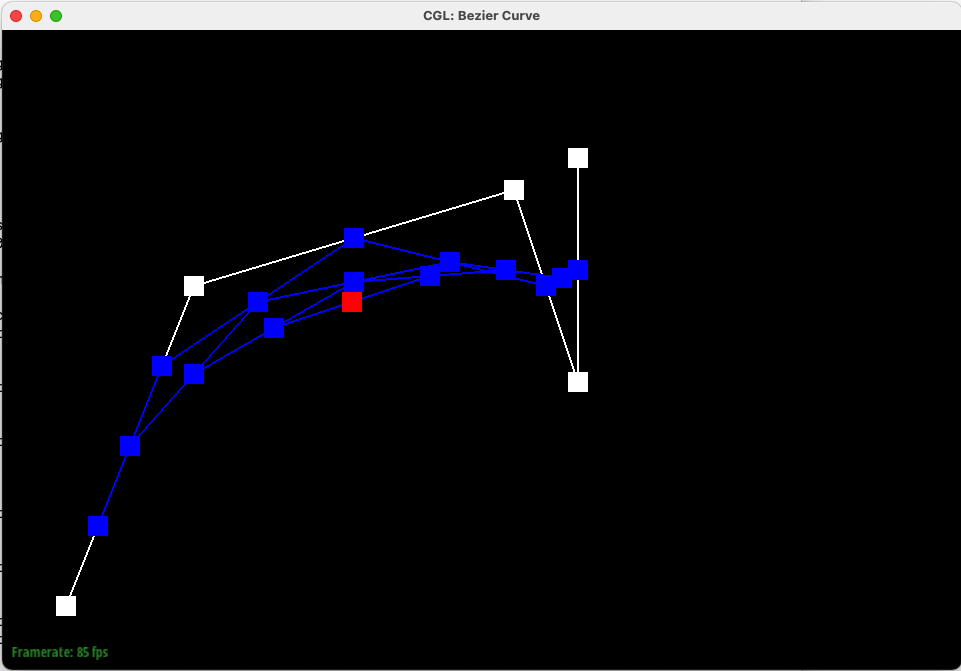
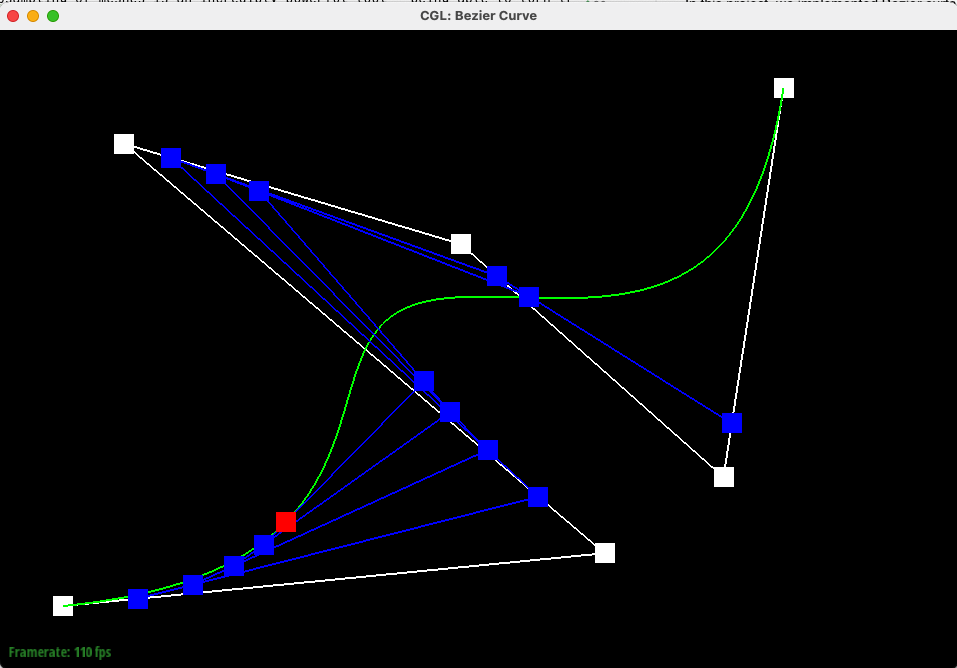
Below are the same control points and algorithm, but generating the entire Bezier Curve (with intermdiate interpolation for different points shown).
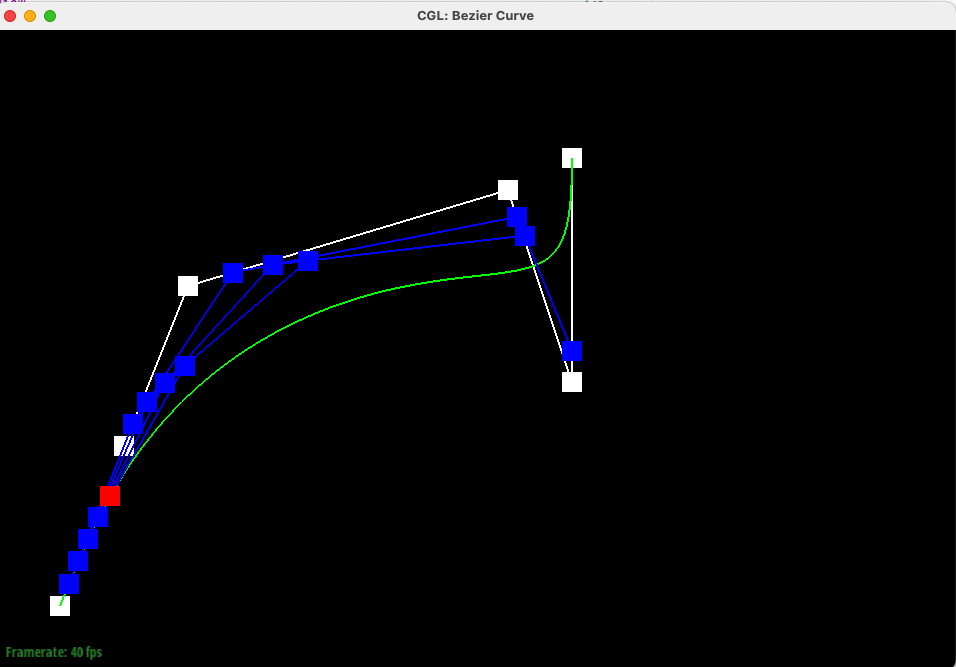
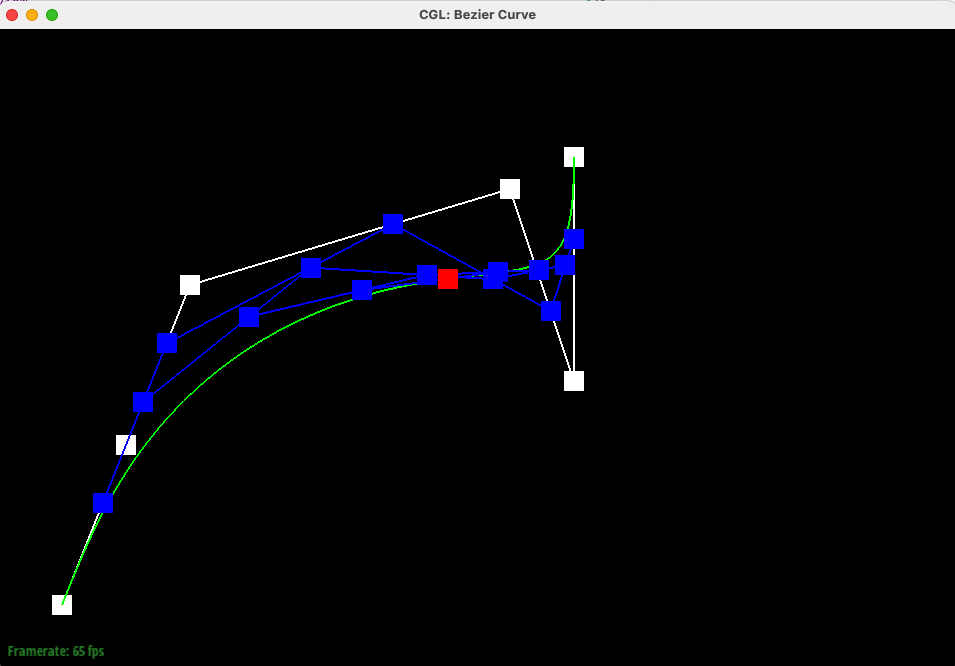
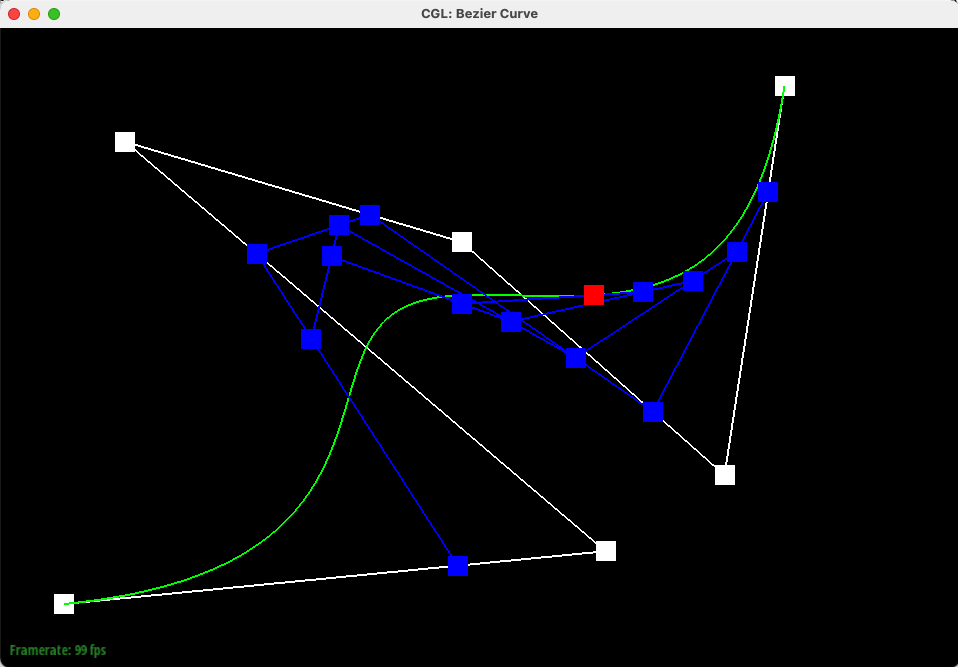
Below is another example with 6 control points, moved from their original positions (with and without intermdiate interpolation shown).
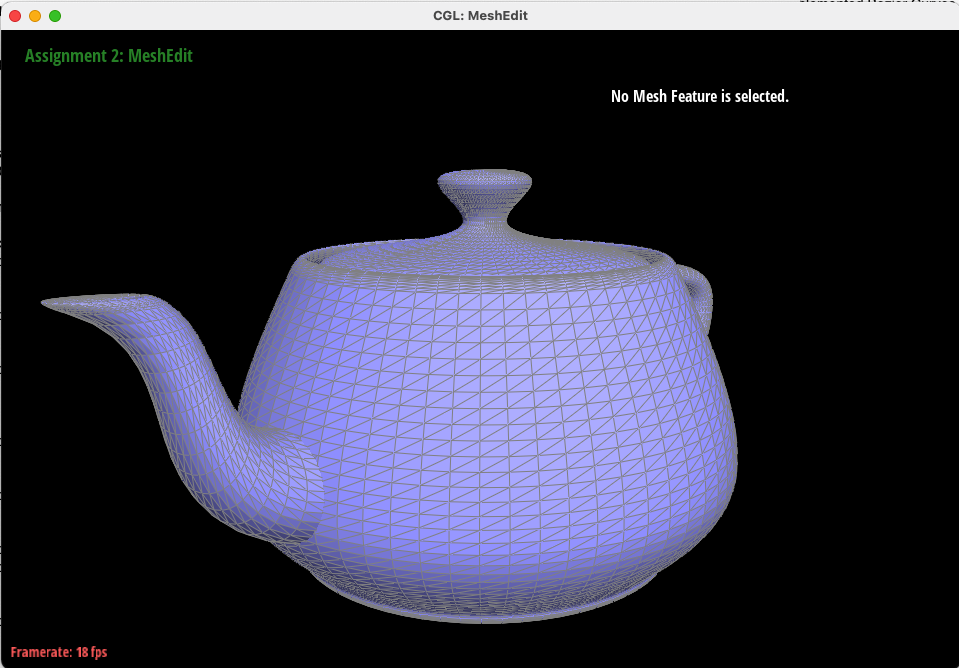
In this task, we implemented Bezier Surfaces with the separable 1D de Casteljau algorithm. Given an m by n collection of control points, we first interpolated for a given point across all m points along one dimension (one row) varying parameter u, and then used the resulting interpolated points to interpolate points on the actual surface across all n rows by varying parameter v. In this way, we were able to interpolate across three dimensions and create a smooth surface efficiently.
Below is the "teapot.bez" rendered using our bezier surface implementation.
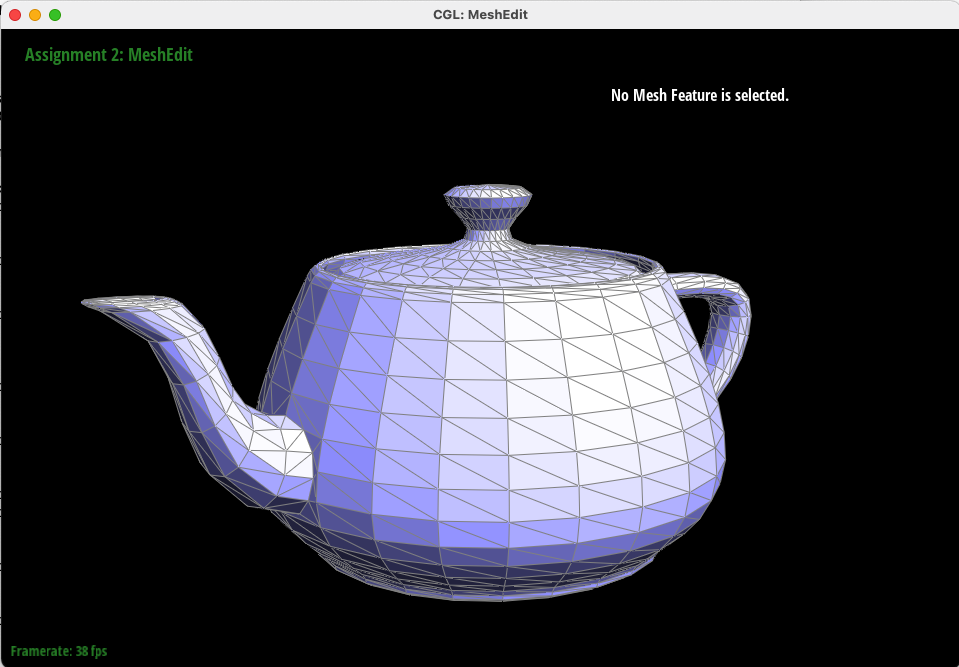
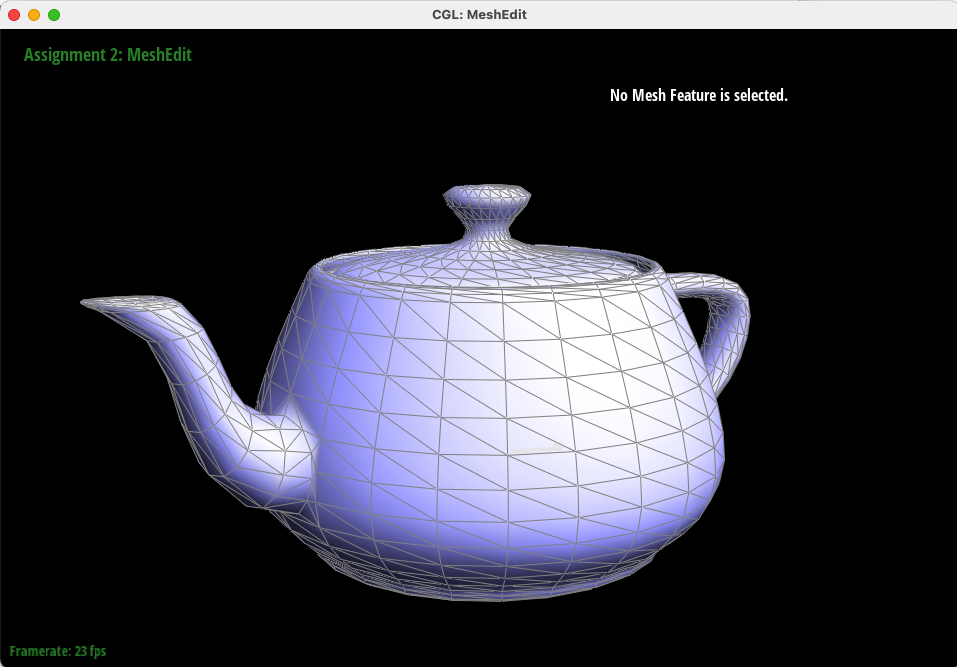
In this task, we implemented area-weighted normal vectors for all vertices to more accurately shade triangles with Phong shading. We accomplished this by traversing all the neighboring faces of a vertex, and calculating the approximate unit normal at that vertex by weighting its neighboring faces' normals by those faces' area.
Below, you can see the difference between flat shading (by triangle) and Phong shading (interpolation by the vertex normals as calculated above) on the "teapot.dae" file.
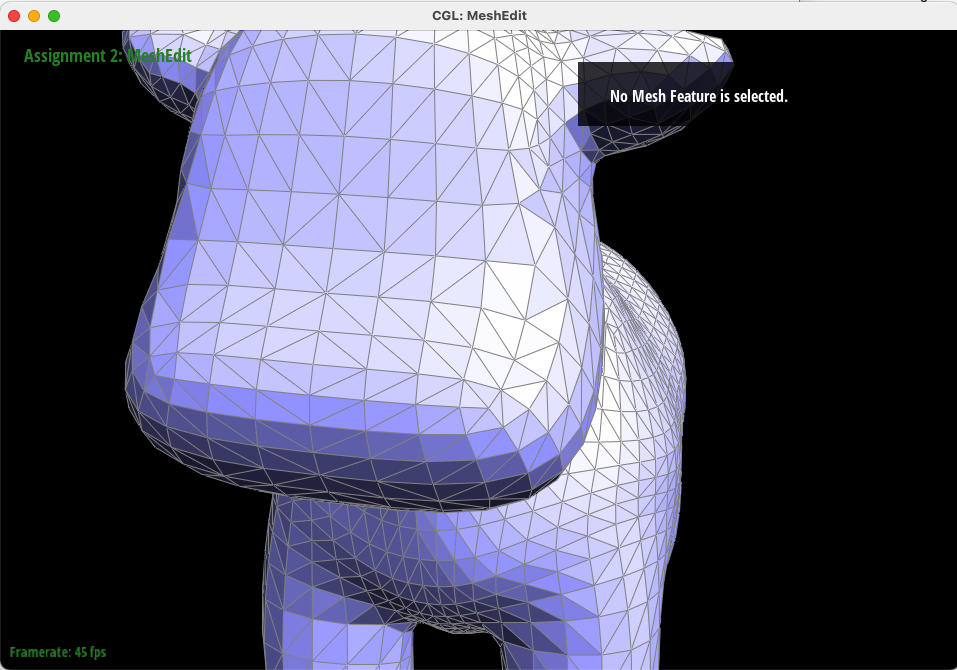
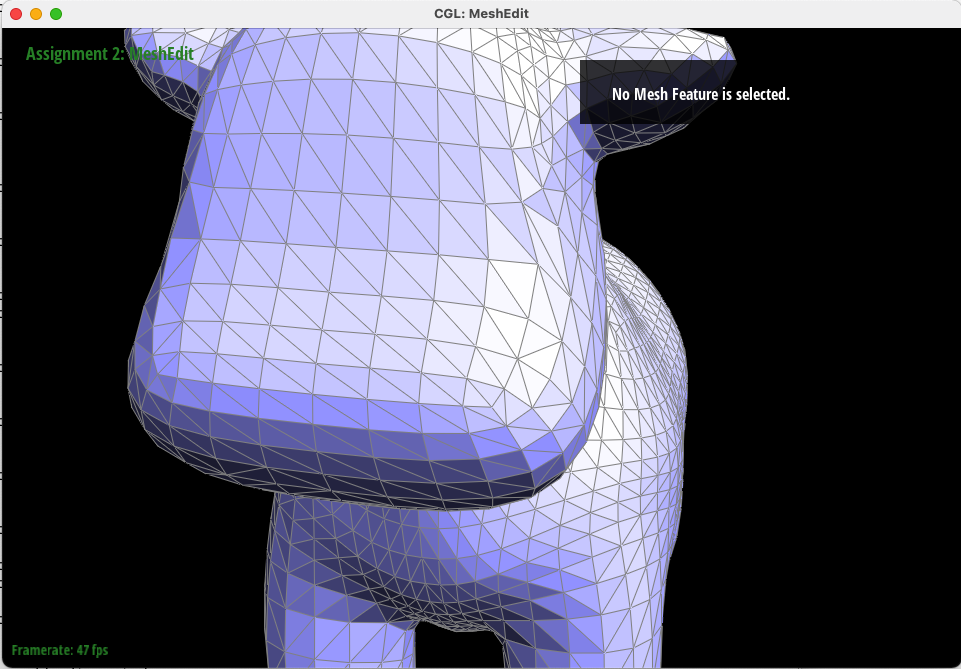
In this task, we implemented the "edge flip" operation to transform two adjacent triangles ABC and CBD into triangles with the same outer edges ADC and ADB by flipping the connecting edge. This was done using the halfEdgeMesh data structure and careful accounting of what pointers within the structure needed reassignment. We preserved the inner edge BC's pointers to related halfedges, basically rotating the two triangles within the confines of the outer edges AC, CD, DB, and BA. Thankfully, after a careful examination of every element, we didn't need any further debugging tools.
Below, "cow.dae" is rendered as specified by the file, and then after a sequence of edge flips to orient the triangles on the face of the mesh the same direction.
In this task, we implemented the "edge split" operation to transform two adjacent triangles ABC and CBD into four triangles ACE, CED, BED, and ABE by creating a new vertex e at the midpoint of the edge CB that connected the two adjacent triangles ABC and CBD. We did this by creating vertex e, preserving edge CB as edge CE, and creating three new edges (DE, BE, AE) and the corresponding faces and halfedges.
By making sure that edge BC remained intact as edge CE, we were able to preserve traversal techniques and guarantee correctness of our edge splits.
Below, "cube.dae" is shown before and after a series of edge splits on its nearest face.
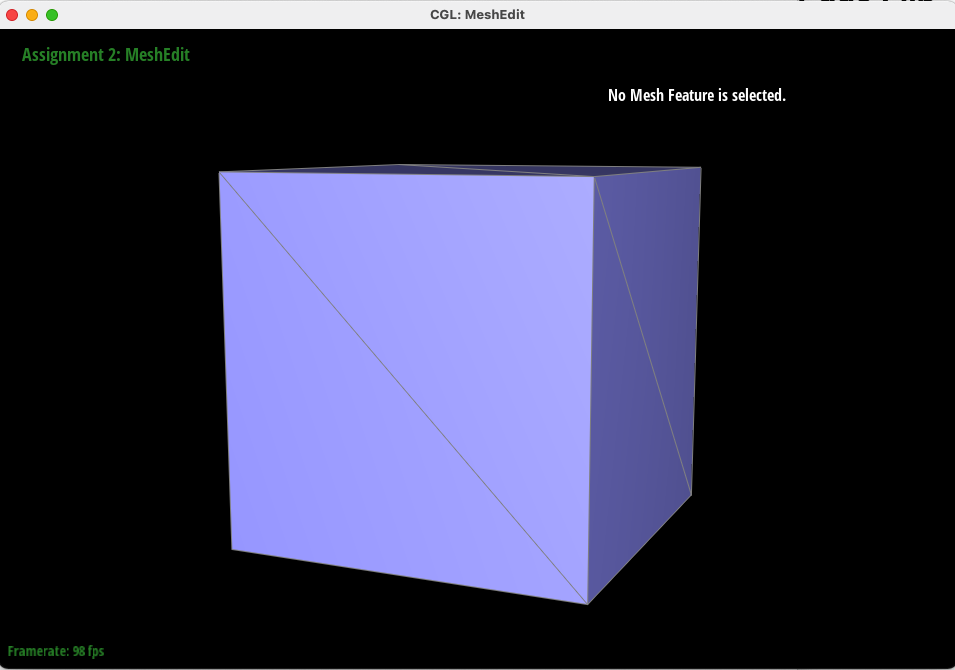
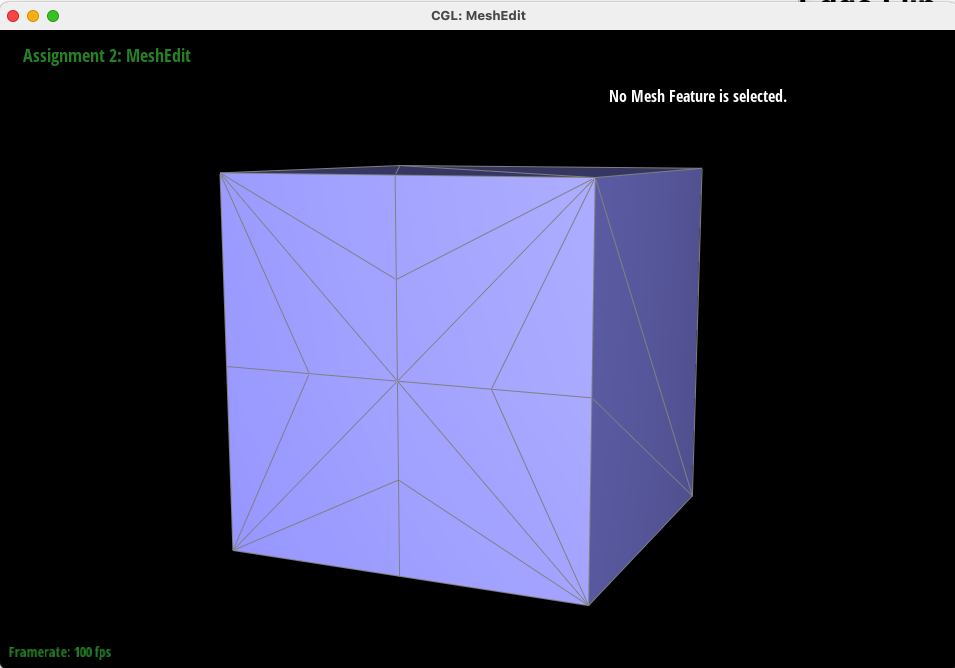
Below, "bean.dae" is shown before and after a series of both edge splits and edge flips.
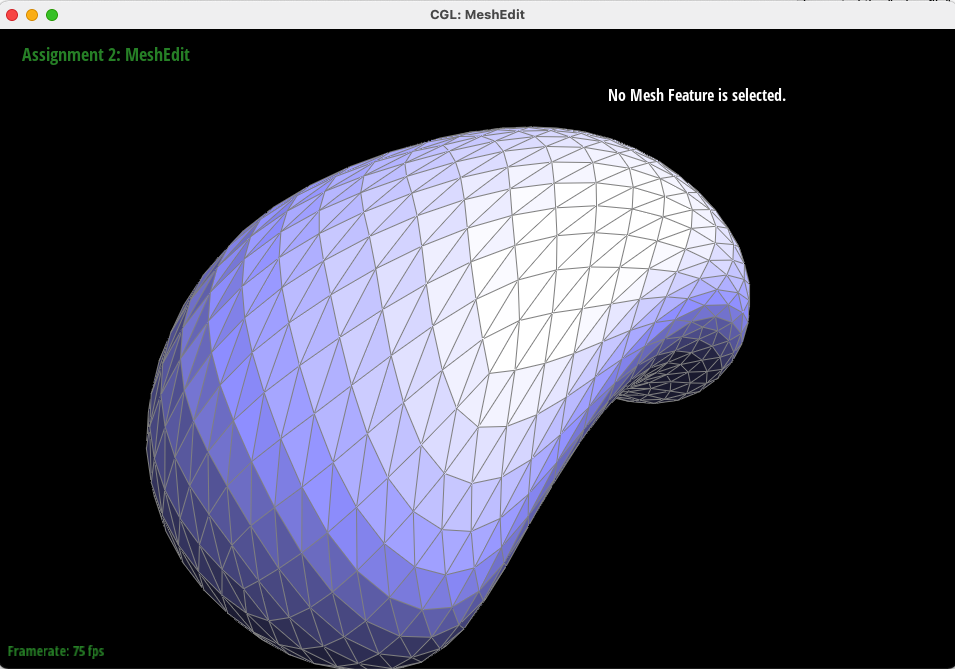
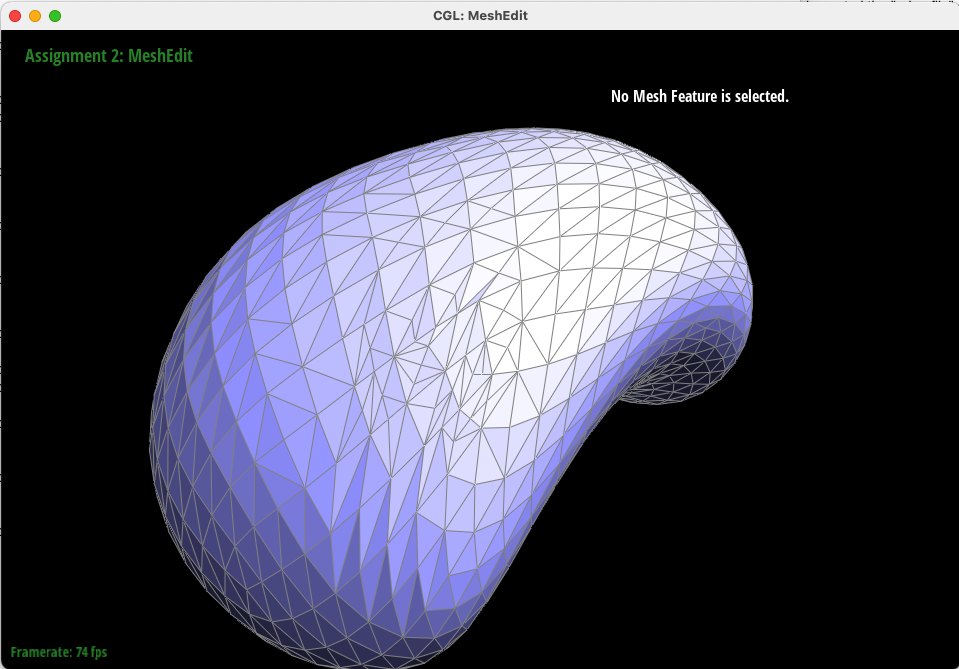
In this task, we utilized the Loop Subdivision algorithm to upsample a mesh. With a series of edge splits and flips across the entire mesh and calculations using vertex neighbors to update positions, this algorithm augments a given mesh to render it in more detail (with more triangles). By adding and updating isNew and isOriginal flags to edges and vertices, we were able to iterate over all edges and vertices of a mesh and appropriately carry out the upsampling algorithm.
Initially, we had an issue where the new position of a vertex created by an edge split was incorrect - causing bizarre artifacts instead of the correct faces touching new vertices. We solved this by transferring the new position at the time of split - not waiting until a later iteration when that vertex's neighboring edge may have been flipped or transformed.
Below, Loop Subdivision is performed on the "torus.dae" file, and it can be seen that the polygon's sharp edges are gradually smoothed with upsampling. However, their fidelity can be lost if those edges were intentionally sharp.

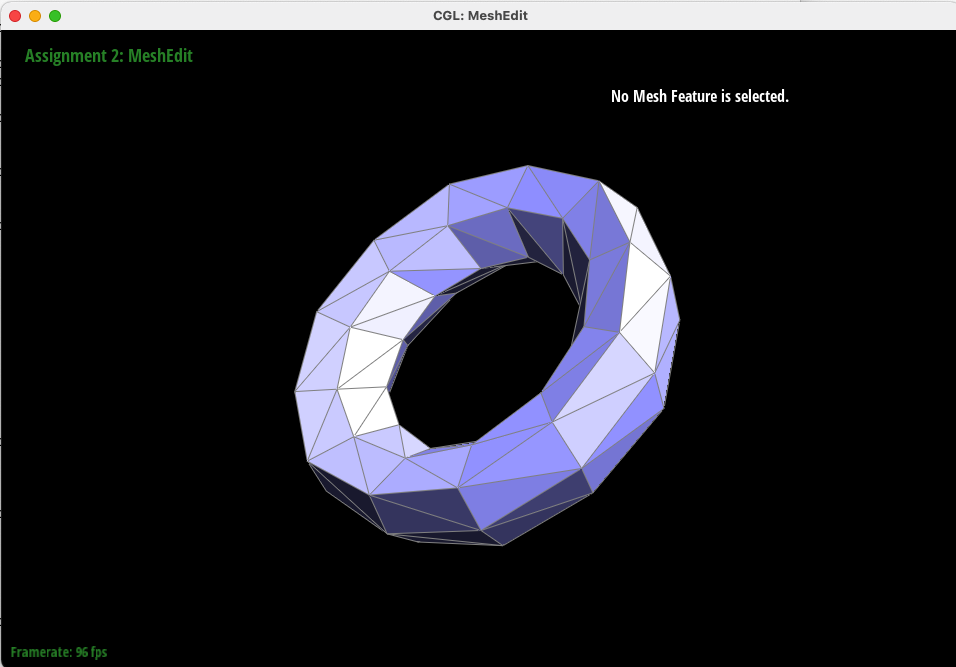

However, by pre-splitting the outer edges of "torus.dae", we were able to preserve the corners of the object! Below are the results of the same upsampling done on the object with pre-split edges.
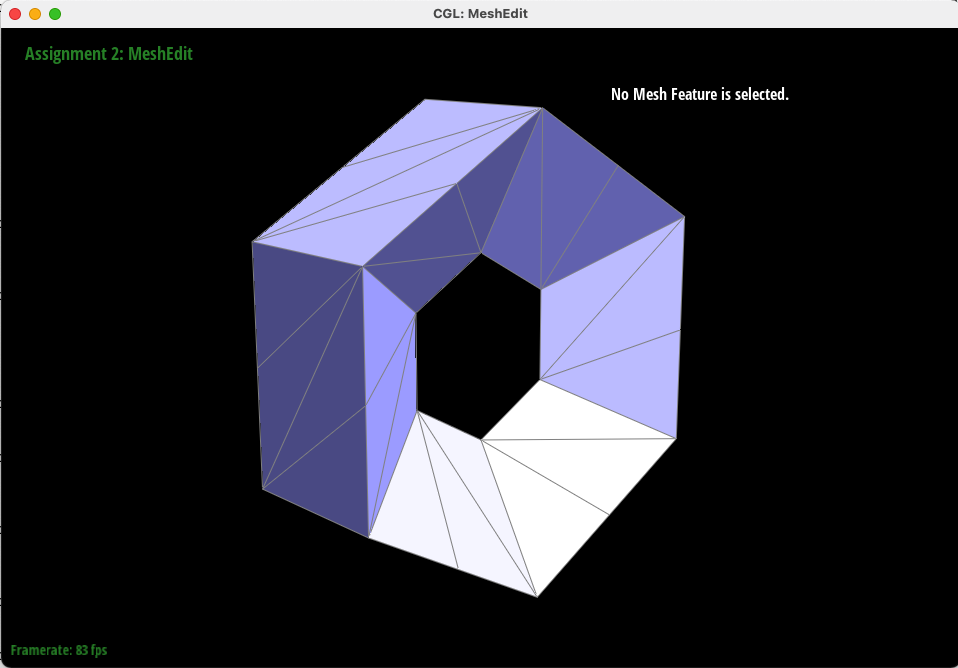
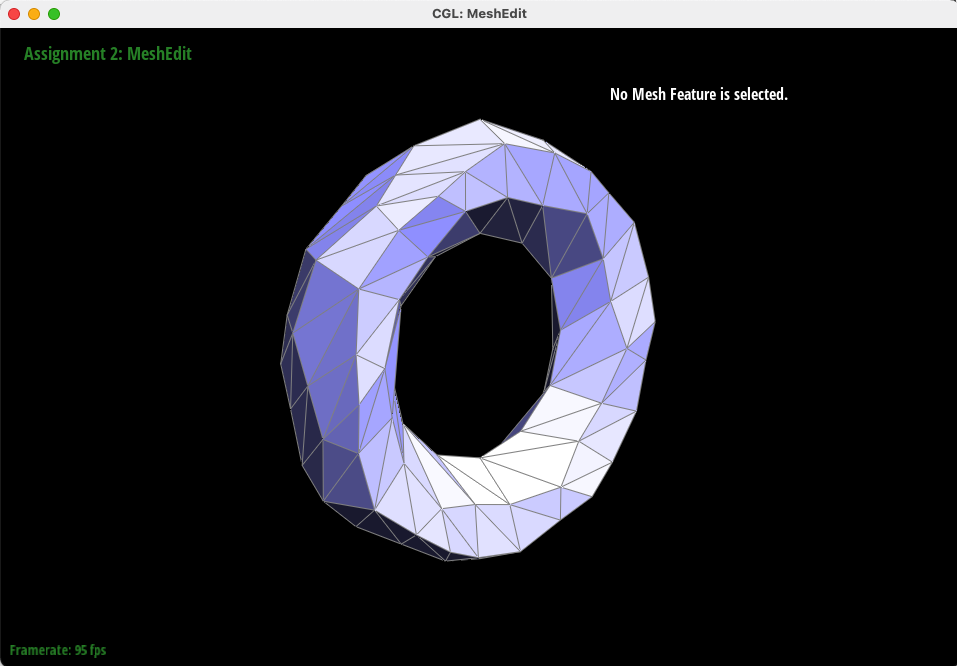
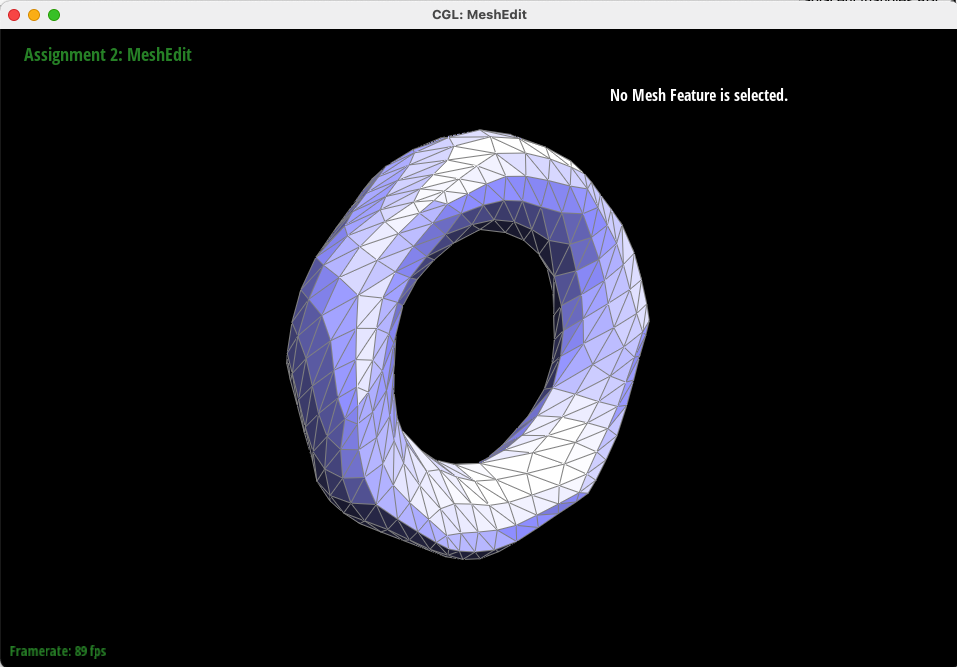
Even for several sequential Loop Subdivisions, the corners are perserved!
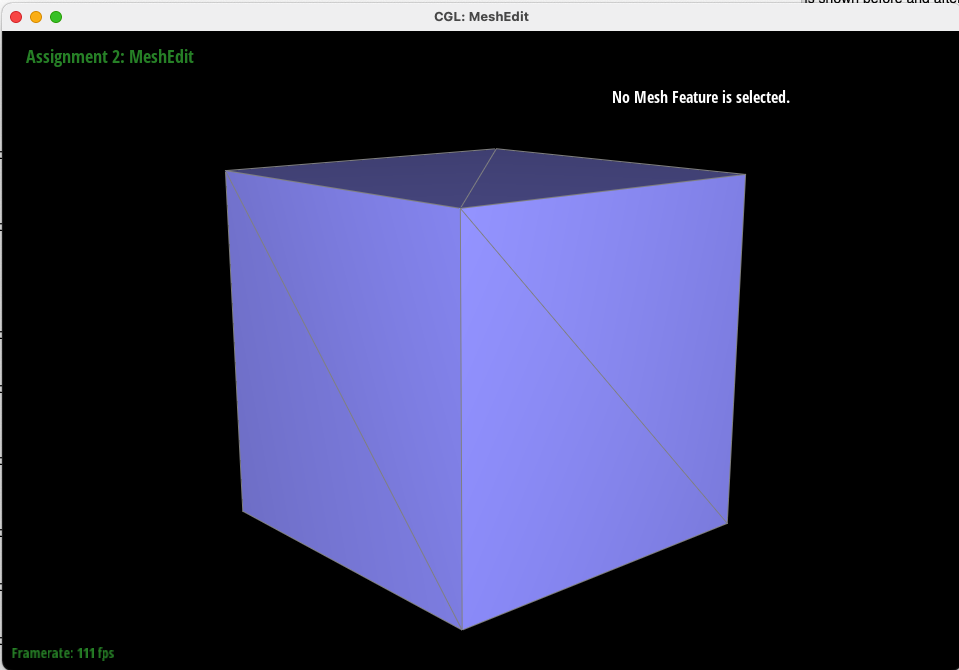
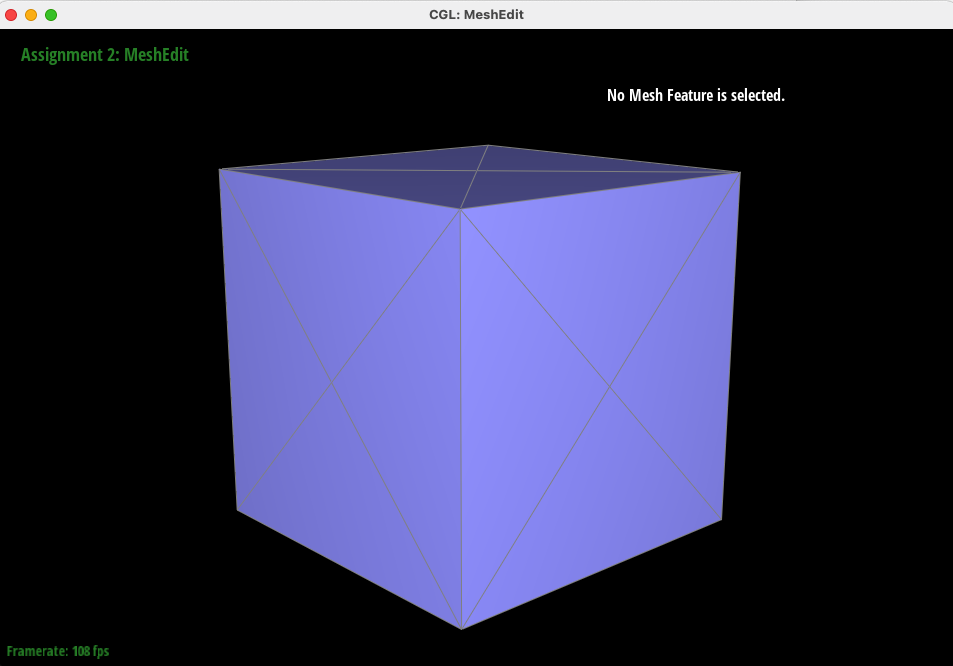
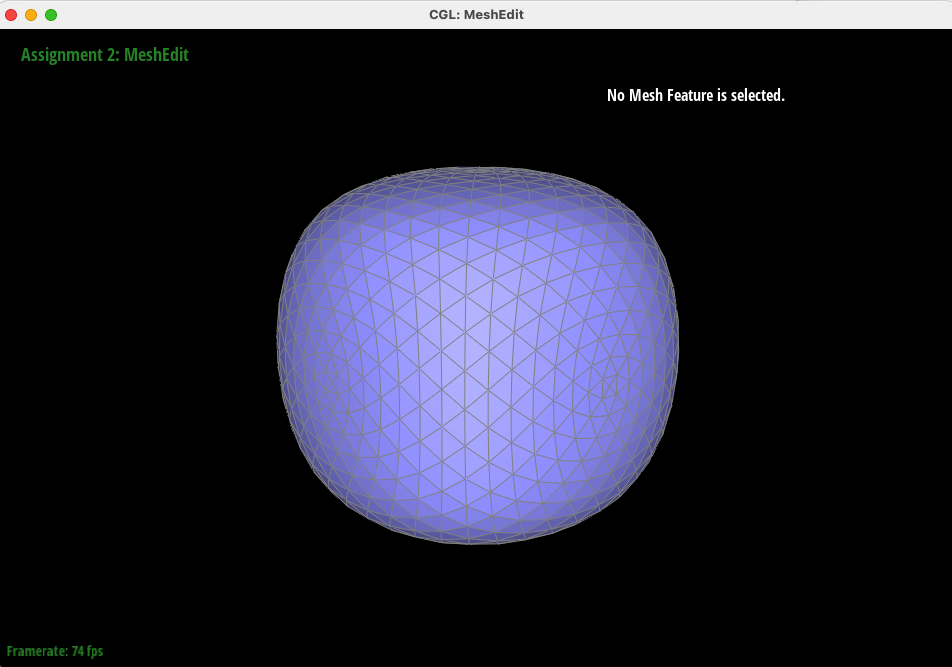
Below, we call Loop Subdivision sequentially on "cube.dae" to smooth the sharp cube into an almost spherical mesh.
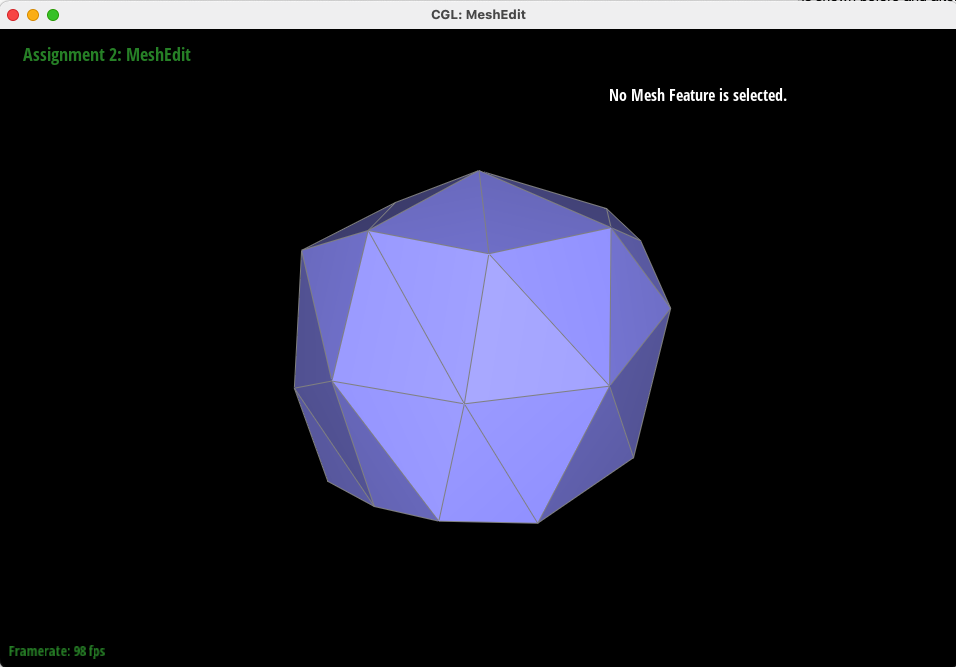
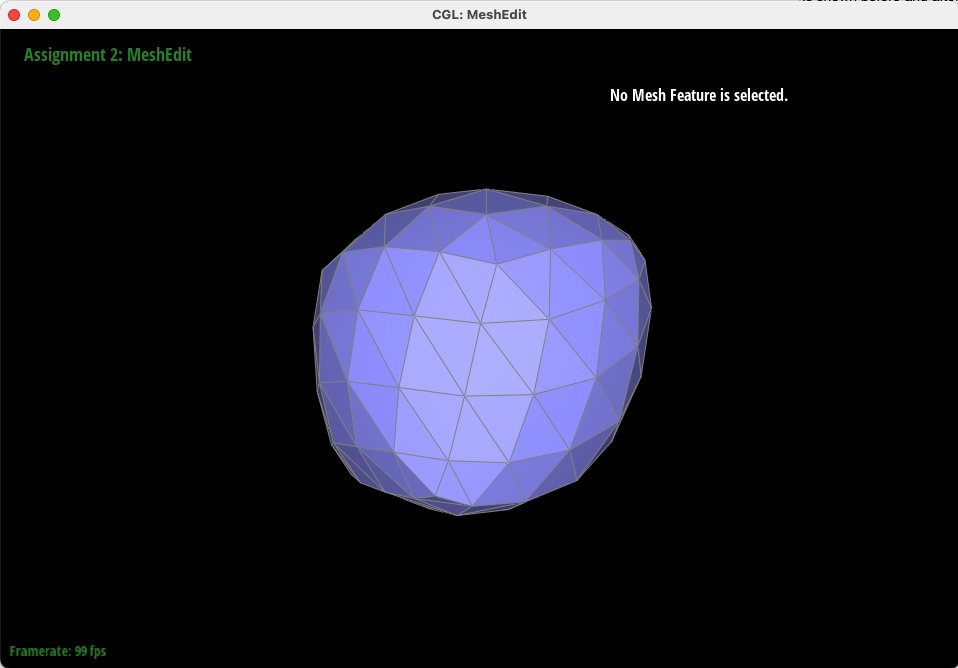
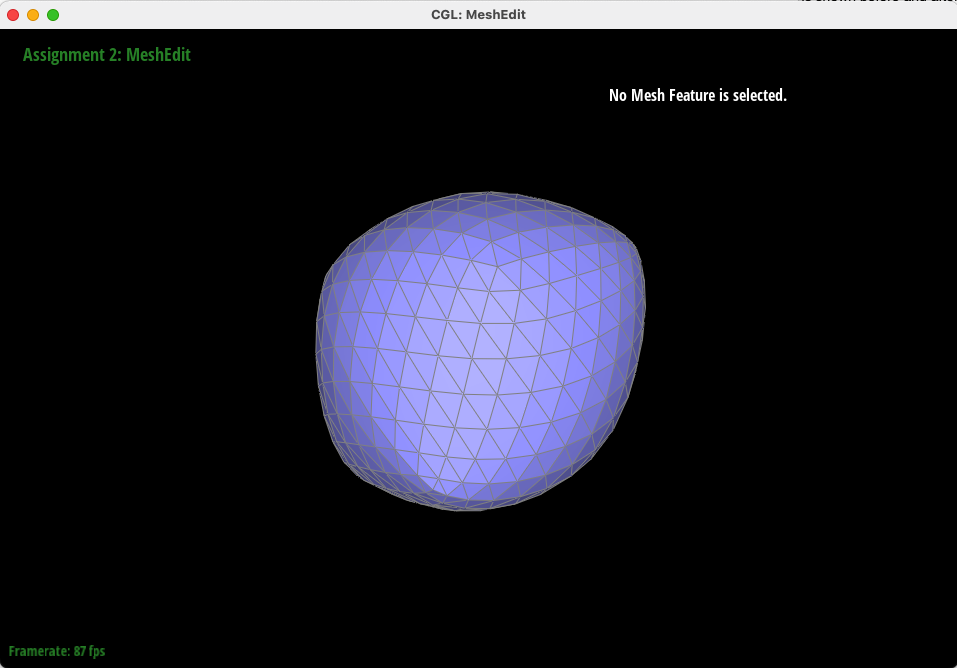
However, splitting the cube with no preprocessing causes asymmetry (two corners protrude more than the others) - and this is because of the degree of each corner vertex! Because of the representation of the face of the cube as 2 triangles, some corners have a higher degree by having more incident edges. Thus, by splitting each face into four equal triangles, we can guarantee that each corner vertex has equal degree, and thus are processed identically by the upsampling algorithm. In this way, we can guarantee that our mesh remains symmetric.
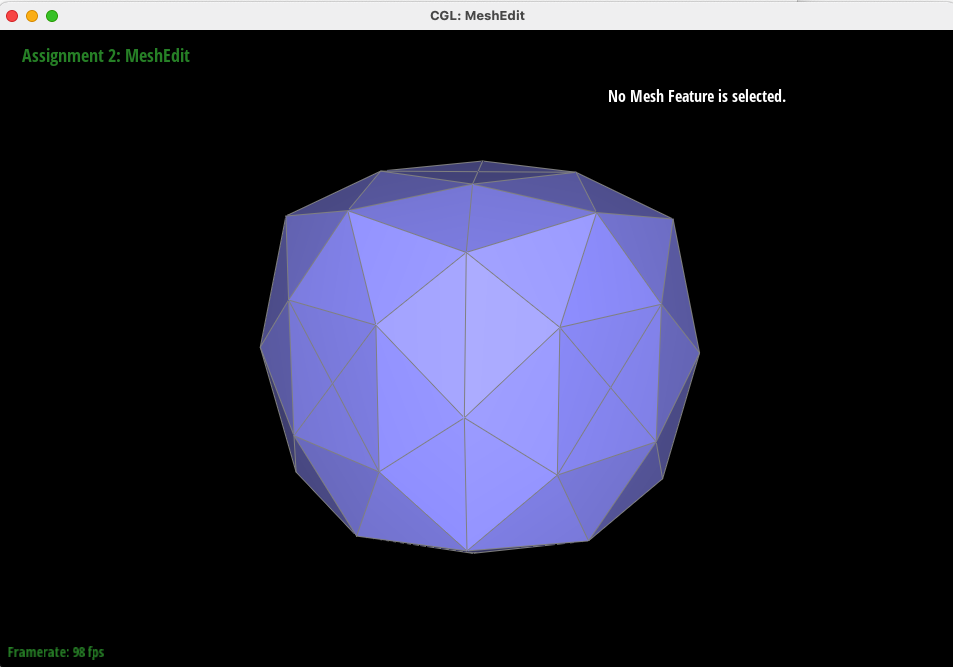
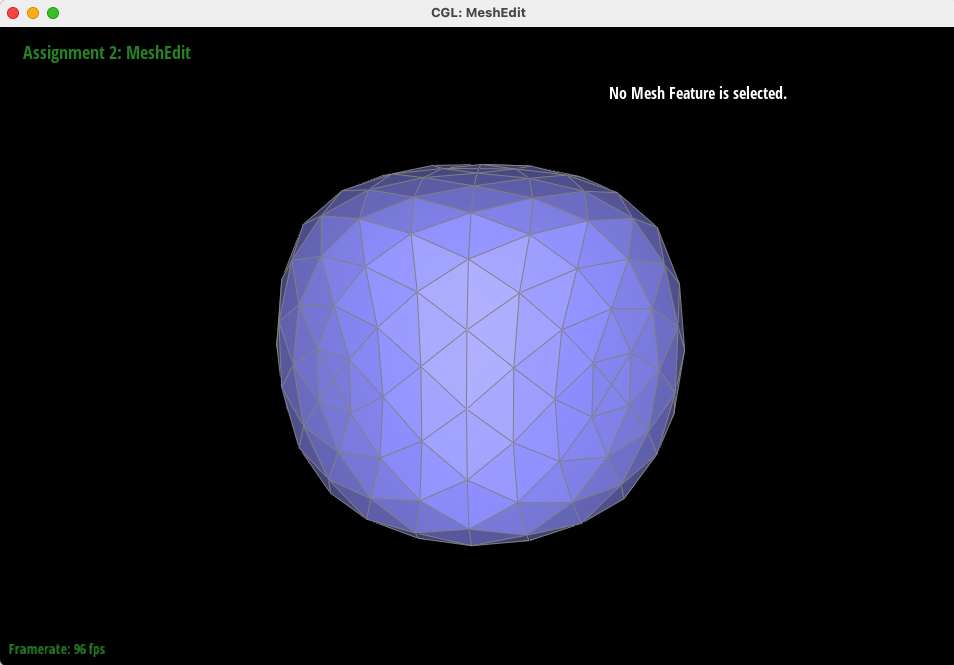
Below is the result of Loop Subdivision given the preprocessing described above.
In utilizing the halfEdgeMesh data structure to implement procedural upsampling and improved shading and rendering of surfaces, it became clear how crucial the data structure is. We thoroughly enjoyed working with the data structure, the linear interpolation of smooth surfaces, and algorithmic upsampling.
The understanding of how symmetry and manifold properties can be affected by our transformations is also important, and was illustrated in great detail by this project.