mesh editor

Nadia Hyder, CS 184 Spring 2021

OVERVIEW

In this project, I explored several geometric modeling concepts; I built Bezier curves and surfaces using de Casteljaus algorithm, manipulated triangle meshes represented by the half-edge data structure (flipping and splitting edges), and implemented loop subdivision for upsampling. This project is split in two sections: 1. Bezier curves and Surfaces, and 2. Triangle Meshes and the Half-Edge Data Structure.

SECTION I: BEZIER CURVES AND SURFACES

Part 1: Bezier curves with 1D de Casteljau Subdivision

I implemented Bezier curves using de Casteljau’s algorithm. Bezier curves run from a start to end point, with its curvature influenced by intermediate control points. Bezier curves are the result of several linear interpolations over lines connecting these points.

De Casteljau subdivision is a divide-and-conquer algorithm for evaluating Bezier curves, recursively performing linear interpolation between two points to place new control points between edges. The base case is when there is only one point left.

More formally, the recursive step is a parametrized equation of the movement between two points. Given n control points p1, …, pn, and the parameter t, we use linear interpolation to calculate the n-1 control points in the next subdivision level:

I implemented this recursive step, which eventually brings us to a final, single point which lies on the Bezier curve given parameter t.

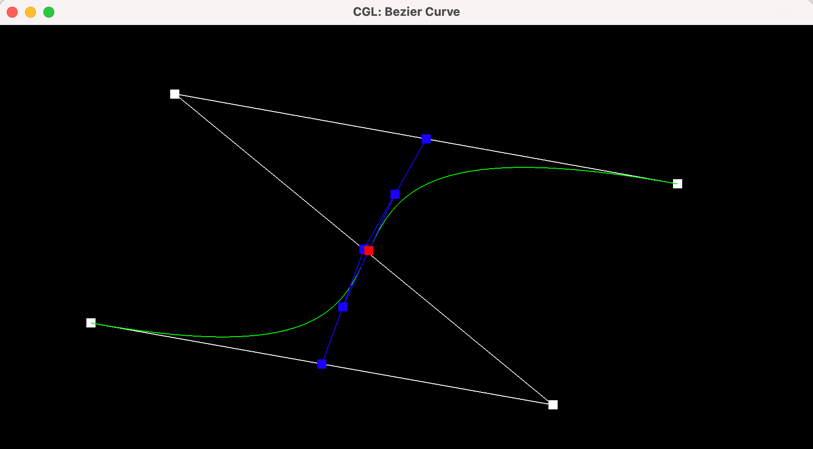
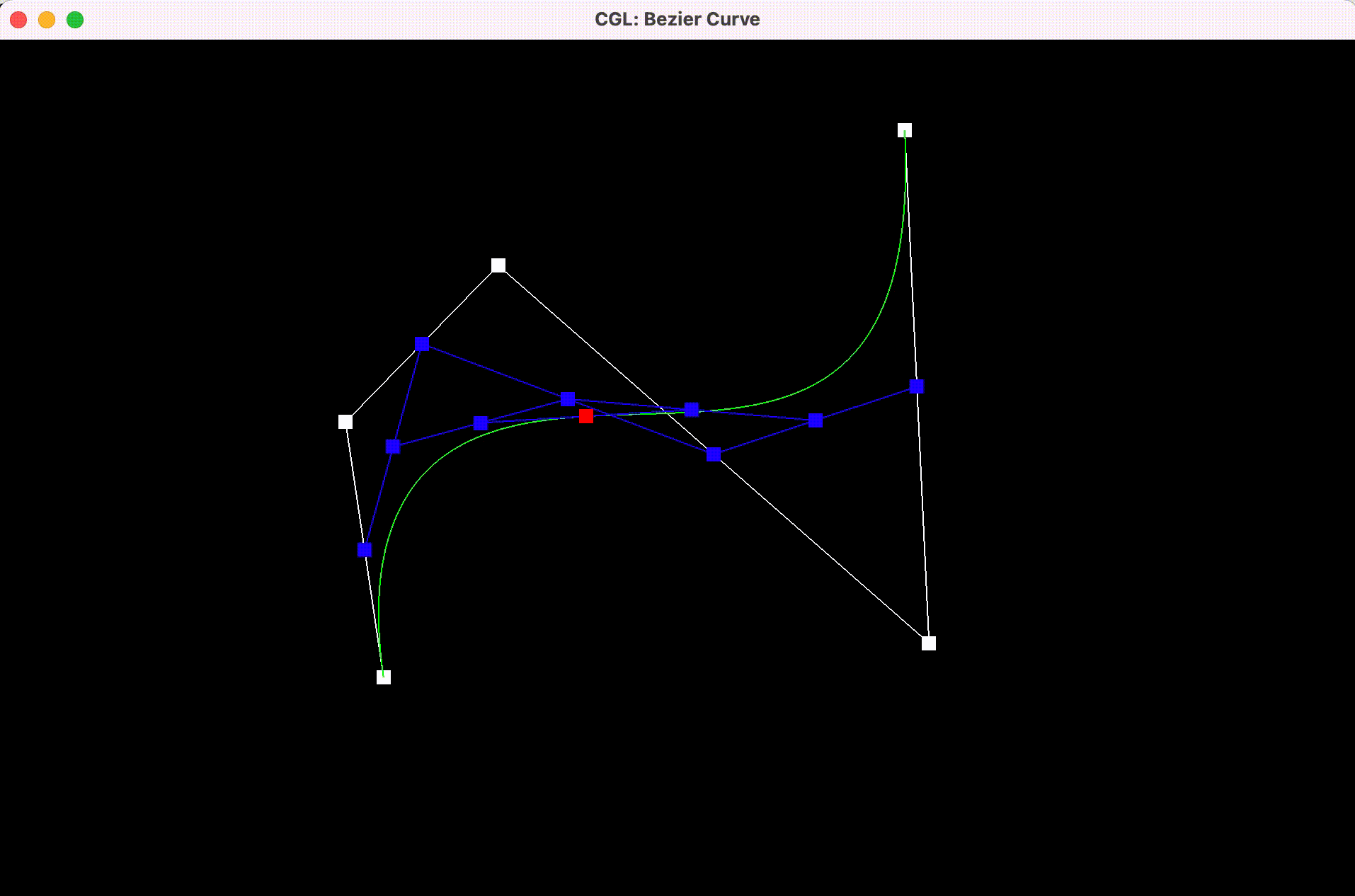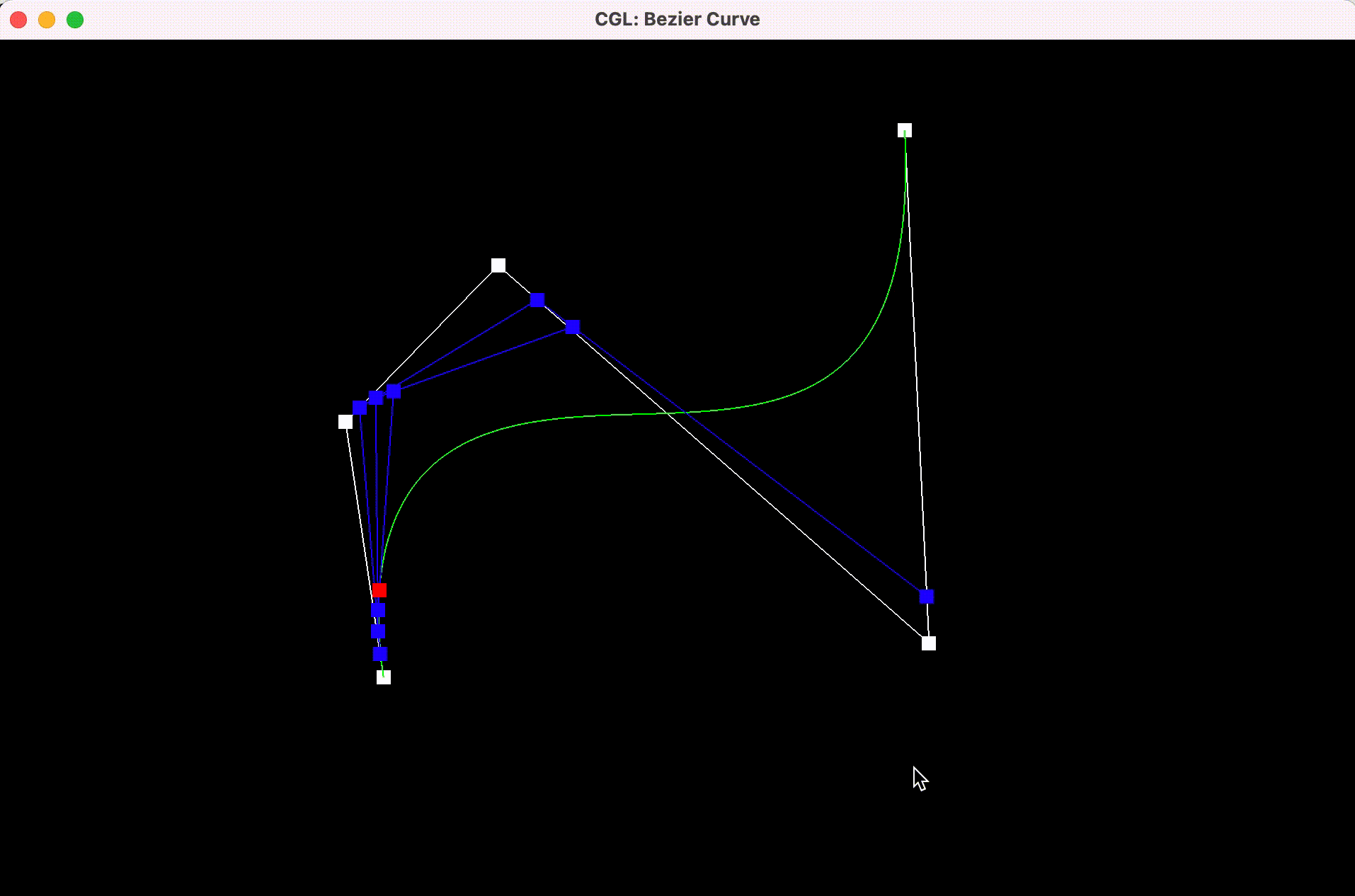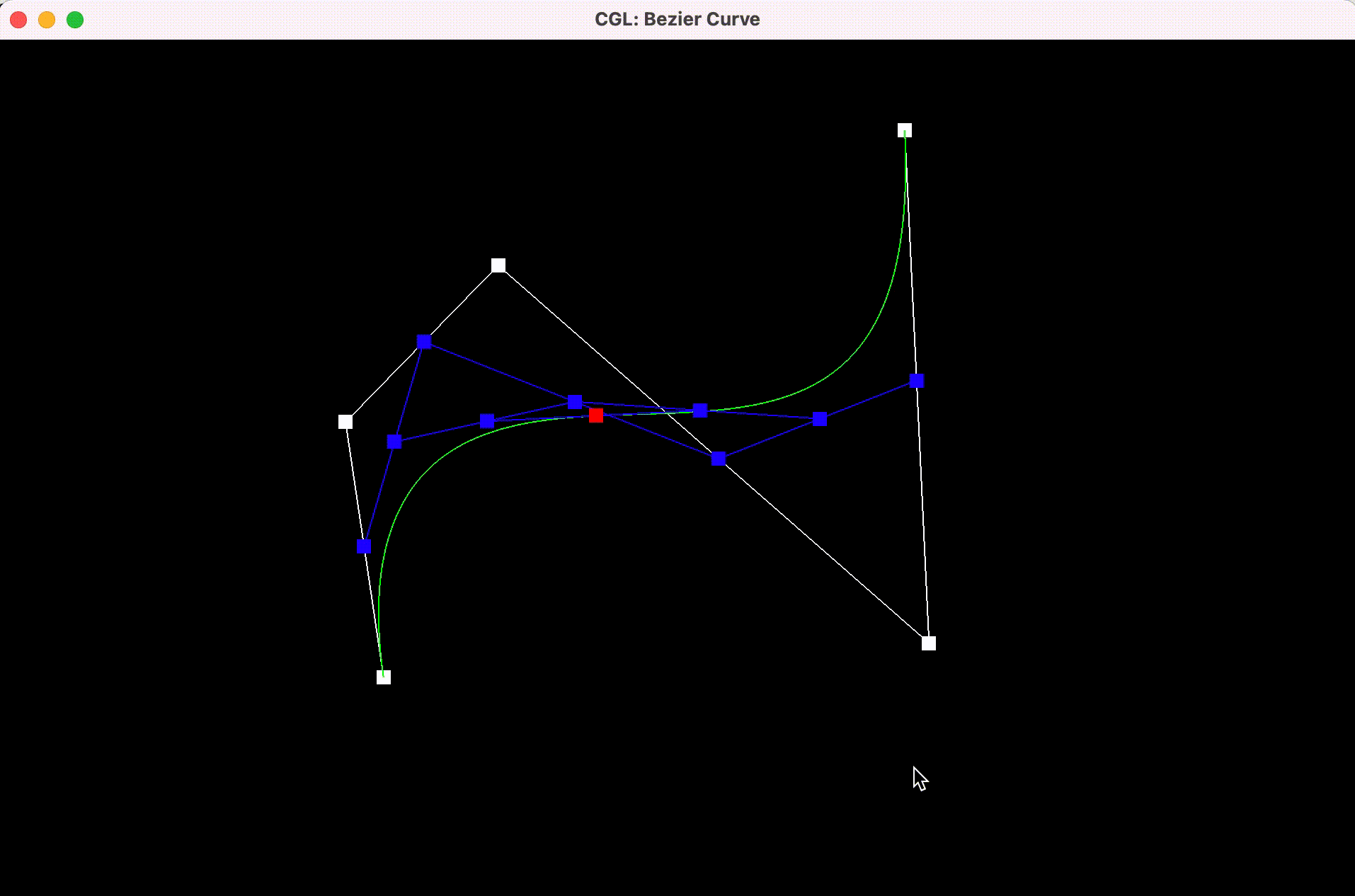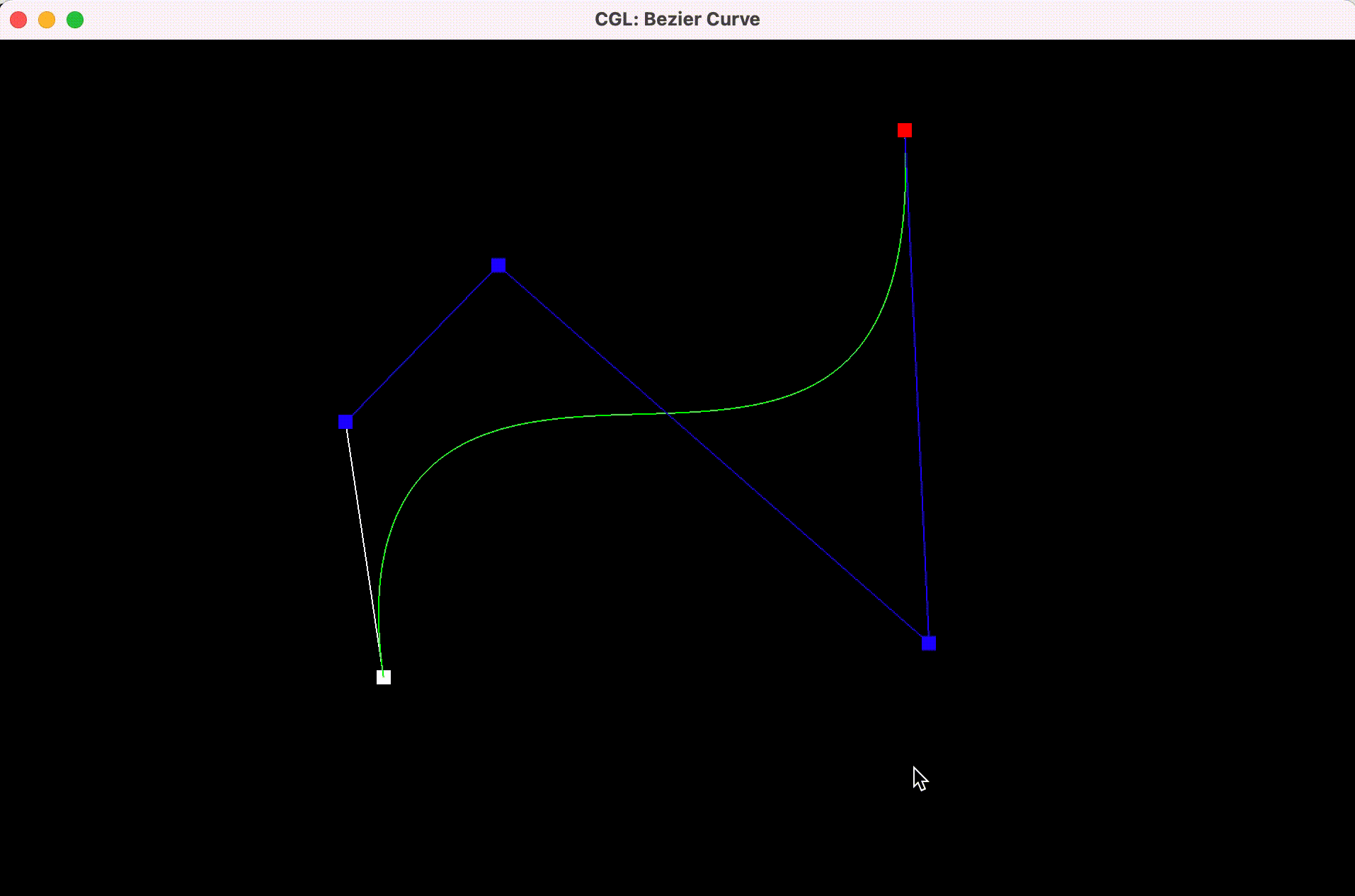
Here are the results:

Bezier curve with each step of the evaluation from original control points to final evaluated point

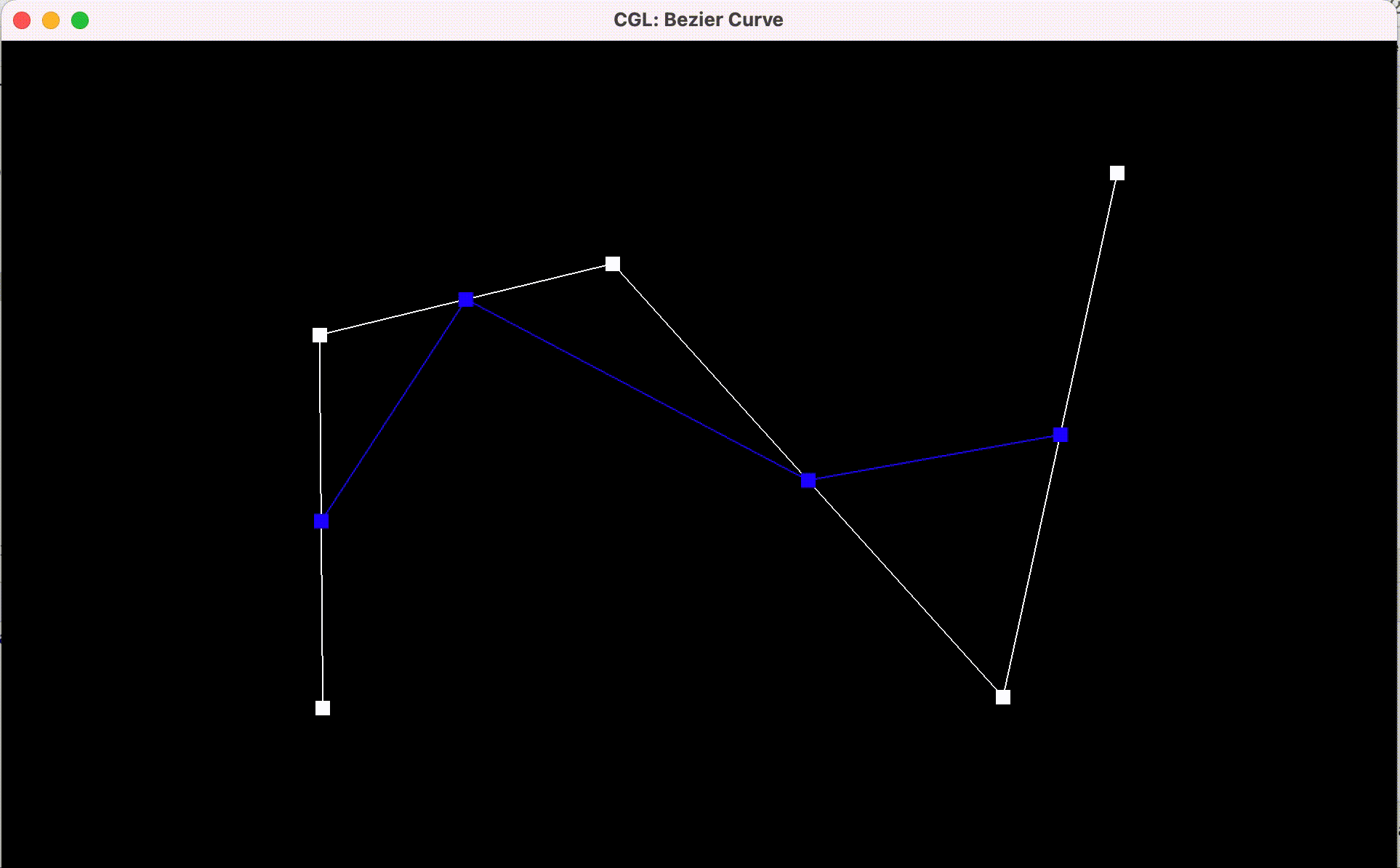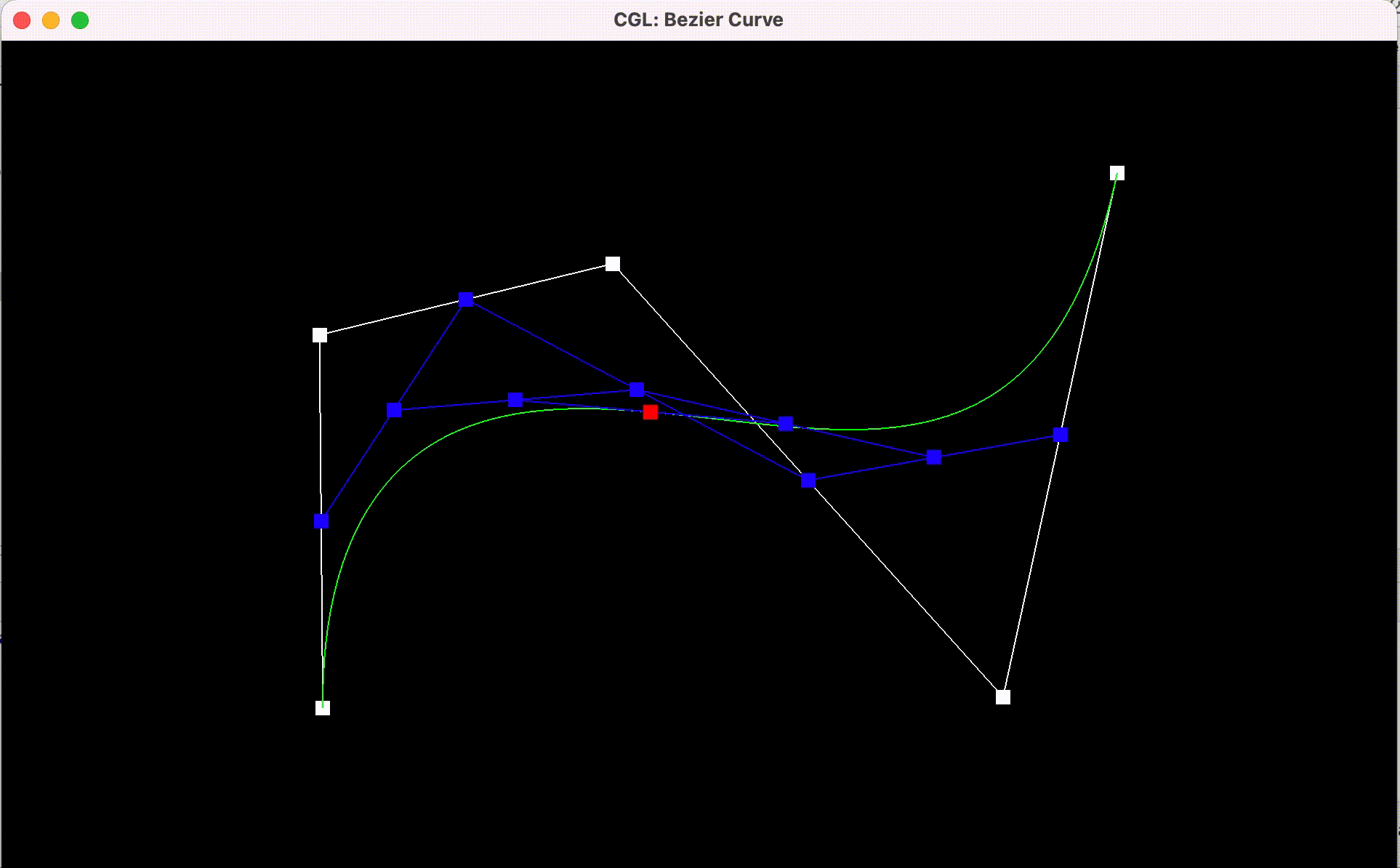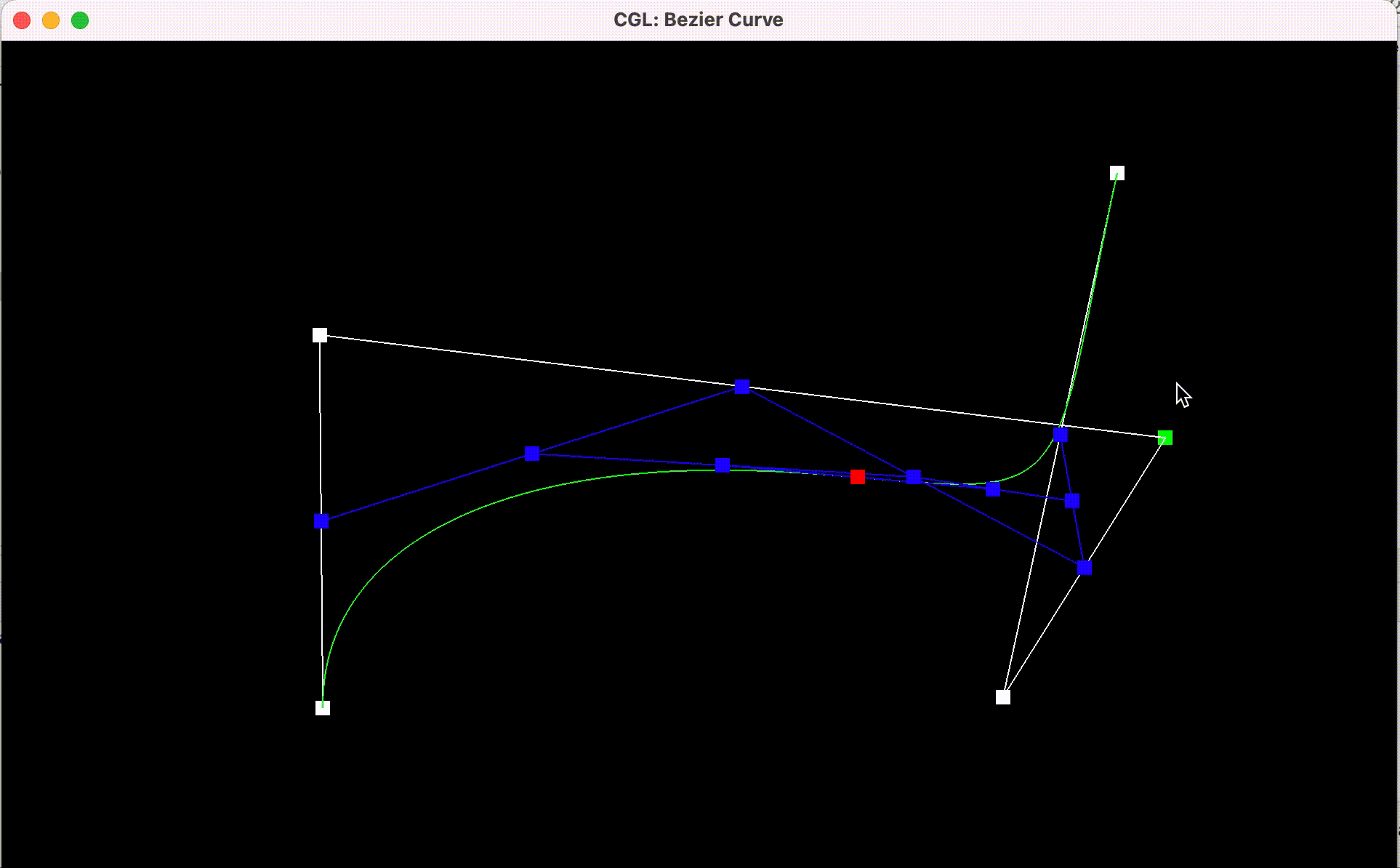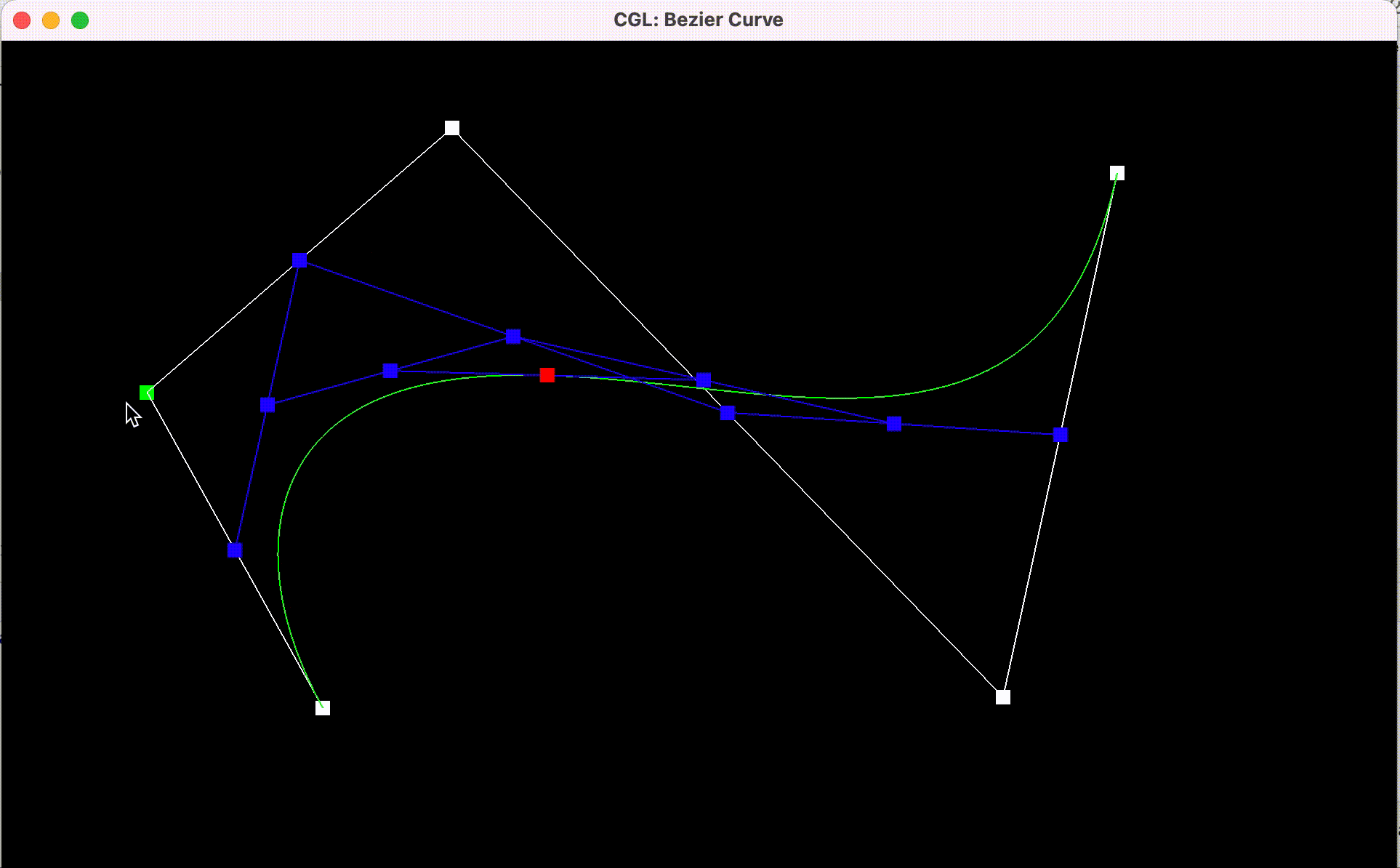
Bezier curve with modified parameter t

Part 2: Bezier surfaces with separable 1D de Casteljau

Next, I applied de Casteljau’s algorithm to Bezier surfaces. Instead of looking at n control points, a surface is defined by and nxn grid of control points, with curves going along the u or v direction. We move along the curves in the u direction and the v direction, both of which span from 0 to 1. A Bezier surface can be computed as a “sum of Bezier curves”.

More specifically, for nxn control points, each nx1 control point Pi in u defines a Bezier curve. These points, Pi, are found using the recursive step from part 1 at the parameter u. The corresponding points on the n Bezier curves define n control points for a “moving curve” in v. Again, using the recursive step from part 1, I evaluated the final, single point { on the Bezier curve at the parameter v. This point P lies on the Bezier surface at the given parameter u and v.

Here is an output: a teapot, with its surface rendered using de Casteljau’s algorithm:

SECTION II: TRIANGLE MESHES AND HALF-EDGE DATA STRUCTURE

In this next section, I worked extensively with the half-edge data structure to represent surfaces using triangle meshes. Triangle meshes are easier to render than Bezier surfaces.

Part 3: Area-Weighted Vertex Normals

I implemented area-weighted normal vectors at vertices to provide better shading for smooth surfaces (rather than flat shading). Given a vertex, I used its half-edge to iterate through faces incident to the vertex and weighted its normal by its area. Finally, I normalized the sum of all area-weighted normals, returning a unit vector (using the unit() function). I computed a given triangle’s normal vector by computing the cross product of 2 edges of the triangle.

Below is the teapot with and without vertex normals:

without vertex normals	with vertex normals

Part 4: Edge Flip

Next, I implemented a flip: a local remeshing operation on an edge.

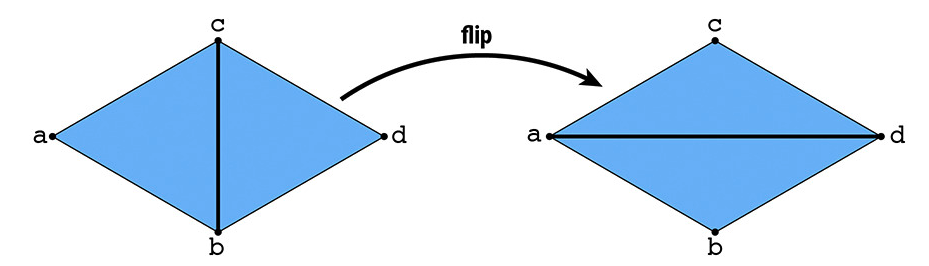
Given an EdgeIter e0 to flip, I had to reassign its twin, next half-edge, vertex, edge, and face. This ended up being quite involved; I first retrieved all half-edges and their twins (for a total of 9 edges, including the given one), all 4 triangle edges, all 4 vertices, and the 2 triangle faces, from e0 and its neighbors. Next, I had to reassign the neighbors for all 9 half-edges, the half-edges corresponding to the edges and vertices, and the half-edges corresponding to the new faces, as appropriate for flipping. I dealt with quite a few bugs in the beginning, because I initially did not account for twin half-edges. I was able to finally come to the correct solution after a few diagram sketches.

Below is the teapot mesh before and after a few edge flips:

before flips	after flips

Part 5: Edge Split

The next local remeshing operation I implemented was an edge split. Splitting an edge inserts a new vertex at its midpoint and yields 4 triangles.

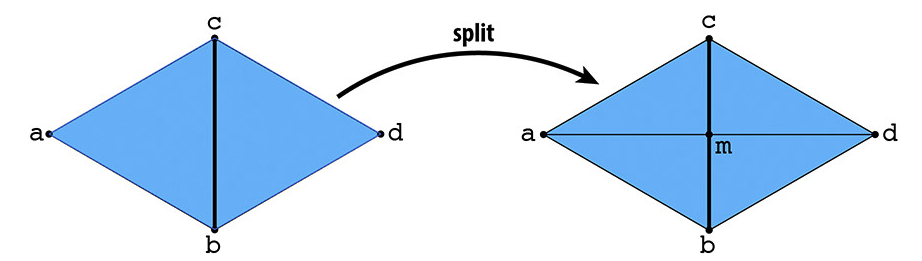
The splitting operation was similar to flipping but required reassigning old half-edge elements and creating new half-edges, vertices, edges, and faces. I first retrieved all half-edges and their twins (for a total of 9 edges, including the given one), all 4 triangle edges, all 4 vertices, and the 2 triangle faces, from e0 and its neighbors. Then I created 6 new half edges (for a total of 15), 3 new edges (total 7), 2 new faces (total 4), and 1 new vertex (total 5). Next, I reassigned all elements to their appropriate half-edge and updated their isNew field when necessary. I defined the vertex as the midpoint between the appropriate vertices. Fortunately, programming the flip operation prepared me well for this part and I did not run into any bugs.

Below are outputs from performing edge splits on the teapot:

before	after edge splits	after edge splits + flips

Part 6: Loop Subdivision for Mesh Upsampling

Finally, I implemented loop subdivision for upsampling. This algorithm is used to convert a coarse polygon mesh into a higher-resolution one. In a loop, I performed the following steps:

1. 4-1 subdivision: subdivides the triangle in the mesh into 4 by connecting midpoints. To do this, I first performed splits on existing edges, then flipped any new edge connecting an old vertex to a new vertex.

2. Vertex position updates as a weighted average of neighboring vertex positions, using the following logic for newly added vertices versus existing vertices:

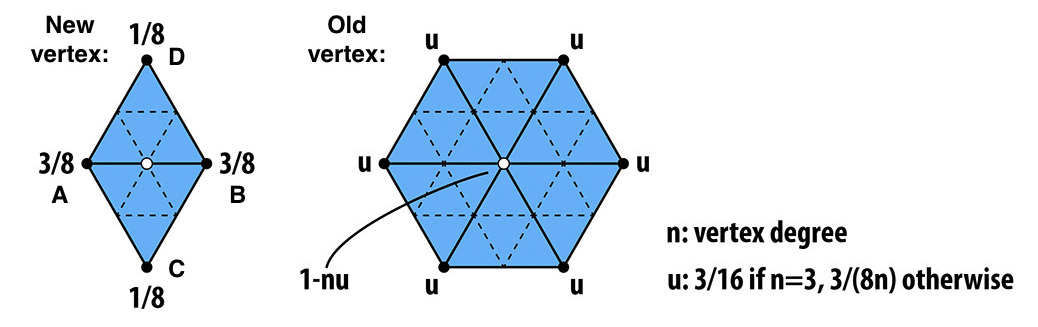
Position of new vertex created when splitting edge AB: 3/8 * (A + B) + 1/8 * (C + D)

Updated position of old vertex: (1 - n * u) * original_position + u * original_neighbor_position_sum where original_position is the original position of the old vertes and original_neighbor_sum is the sum of all original positions of neighboring vertices.

I implemented this algorithm using the following steps: 1. Computed vertex positions using the original mesh, 2. 4-1 subdivision, 3. Updated vertex positions using already computed values.

The only issue I ran into was determining which edges to flip, until I realized I could use xor to make sure only one of 2 vertices was new.

Below is an animation of the teapot after 3 iterations of loop subdivision. This yielded a smoother, rounder mesh with a significantly higher resolution.

Upsampling smoothed out corners and edges and caused asymmetry. This effect is even more noticeable when looking at the following cube:

Turns out, we can reduce the effects of smoothening and asymmetry by splitting interior edges. To keep the cube more symmetrical, I split the interior edges of each face. Having more than 1 edge per face helps better preserve symmetry. The following is a pre-split cube, upsampled 3 times.

CONCLUSION

This project offered me incredible insight into the world of computer graphics and geometric modeling. And yet again, I got to see the power of triangles. This was overall a very enjoyable project and I learned a lot in the process!