rasterizer

Nadia Hyder, CS 184 Spring 2021

OVERVIEW

In this project, I implemented a vector graphics renderer for simplified Scalar Vector Graphics (SVG) files. I implemented several functionalities and features including triangle rasterization, supersampling, hierarchical transforms, and texture mapping with antialiasing.

TASK 1: DRAWING SINGLE COLOR TRIANGLES

I first created a simple, single-color triangle rasterizer using 2D sampling. To perform 2D sampling more efficiently, I traversed pixels within the given triangle’s bounding box (determined by finding minimum and maximum vertex x and y coordinates), only filling pixels with centers within the triangle.

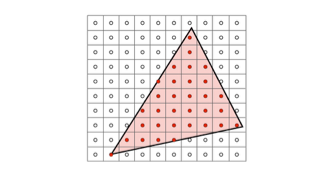
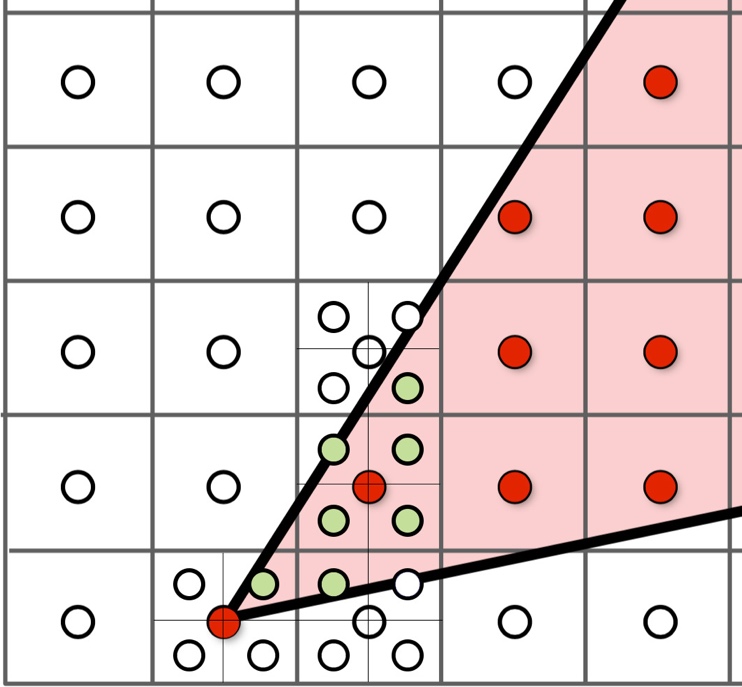
To check if a pixel (or in this case, center of a pixel: x+0.5, y+0.5) was inside the triangle, I implemented a three line point-in-triangle test. Given vertices , , , and some point , we can compute line equations to check if a point is inside, outside, or on an edge:

=

	:	point on edge
	:	outside edge
	:	inside edge

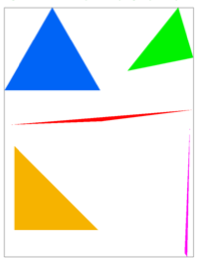
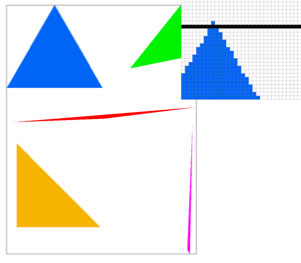
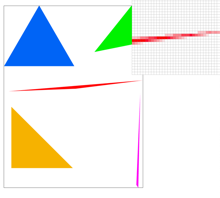
Below are 2 images: the output of triangle rasterization using 2D sampling, and the output zoomed in on the tip of the blue triangle.

TASK 2: ANTIALIASING BY SUPERSAMPLING

Next, I performed antialiasing by supersampling, or sampling several times per pixel (determined by the sample_rate). The results from task 1 show that sampling once per pixel creates sharp edges/ artifacts (also known as jaggies) in the raster image from aliasing, whereas supersampling produces a better raster image yielding smoother edges.

Supersampling required several modifications to the rasterization pipeline. While traversing over the triangle’s bounding box, I also traversed sample_rate # of subsamples for each pixel, checking whether the center of the subsample was within the triangle. If so, I added the subsample to a sample buffer (as opposed to filling the entire pixel like in task 1). The sample buffer is dynamically sized to manage memory appropriately.

Finally, to resolve the supersamples to the framebuffer, I downsampled to width x height final pixels by averaging down the grid of sample values for each pixel in the sample buffer. These final pixels were written to the framebuffer.

Overall, supersampling allowed for more precision and averaging and downsampling pixel values yielded smoother edges and fewer jaggies. The effects as the sample rate increases are considerable. Below is the output of antialiasing by supersampling using sample rates 1, 4, and 16, zoomed in at the right vertex of the red triangle:

sample_rate = 1	sample_rate = 4	sample_rate = 16

TASK 3: TRANSFORMS

Next, I implemented 3 transforms using homogenous coordinates: translate, scale, and rotate. On the left is the original cubeman, and on the right is the cubeman running, after a few transformations are applied.

TASK 4: BARYCENTRIC COORDINATES

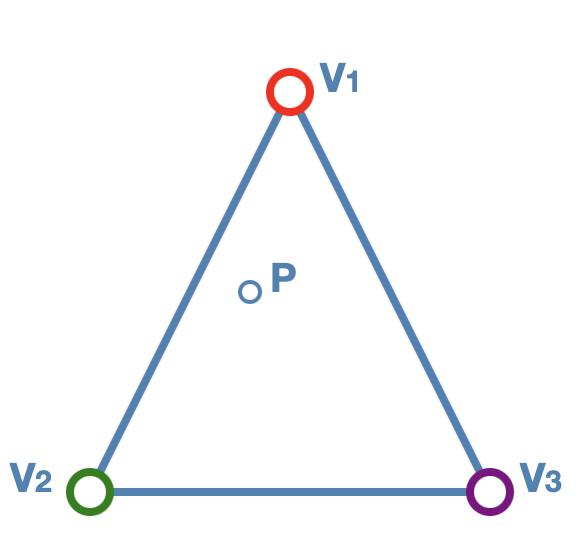
Next, I used barycentric interpolation to rasterize and fill triangles given only vertices and their colors. Given a point P within a triangle, Barycentric interpolation provides a balanced system of equations to find weights for v1, v2, and v3 that tell how much of P’s coordinates are made of v1, v2, and v3. These weights are found using the following equations:

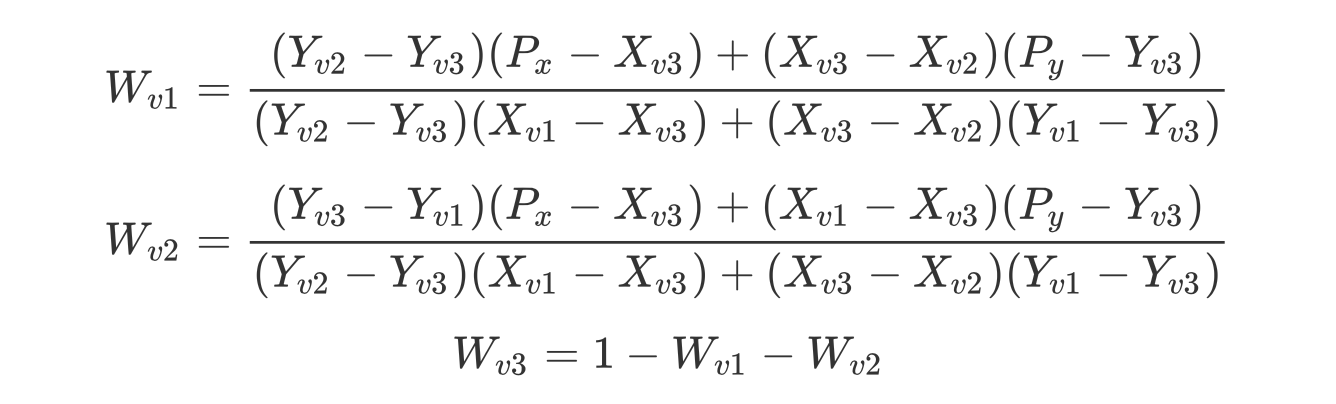
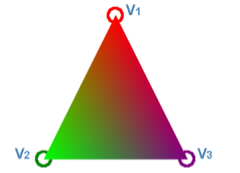
After interpolating the colors at vertices v1, v2, and v3 with their weights w1, w2, and w3, we achieve the following output:

The following is another output produced using the same logic with default viewing parameters and a sample rate of 1:

TASK 5: “PIXEL SAMPLING” FOR TEXTURE MAPPING

I used pixel sampling to perform texture mapping. In pixel sampling, we create a mapping from a texture triangle’s uv coordinates to its barycentric coordinates in order to map a texture to its appropriate color.

There are 2 methods for pixel sampling:

1. Nearest – selects the texture of the closest sample in the texture to the given uv coordinate

2. Bilinear interpolation – uses a weighted average of the 4 nearest samples to perform 2 rounds of linear interpolation (horizontally and vertically).

Bilinear sampling performs better than nearest sampling in several cases; sampling only the nearest texel can miss lines and relevant texels, causing discontinuities. Comparing the images below elucidates this. The image on the left shows nearest sampling and the image on the right shows bilinear sampling, both with a sample rate of 1. There are clear gaps in lines produced by nearest neighbor sampling, while lines are contiguous and smoother when using bilinear sampling.

nearest pixel output	bilinear output

Below are a few more outputs:

nearest sampling, sample_rate = 1	nearest sampling, sample_rate = 16

bilinear sampling, sample_rate = 1	bilinear sampling, sample_rate = 16

We can see clear differences as explained before. Supersampling/ antialiasing creates smoother lines in both cases, so increasing the sample rate improves performance. Furthermore, these output images reinforce that bilinear sampling is better at maintaining continuity as opposed to nearest sampling.

TASK 6: “LEVEL SAMPLING” WITH MIPMAPS FOR TEXTURE MAPPING

Finally, I implemented level sampling to perform texture mapping by mipmap level. In level sampling, we sample from mipmap levels (of an image pyramid where each level has a progressively lower resolution than the previous one). Using lower resolution versions of the same texture saves computation and avoids aliasing caused by high frequencies.

To perform level sampling, I passed the barycentric coordinates of (x+1, y) and (x, y+1) to find its uv coordinates, and calculate du/dx, dv/dx, du/dy, and dv/dy. I calculated the mipmap level using the following logic and formula:

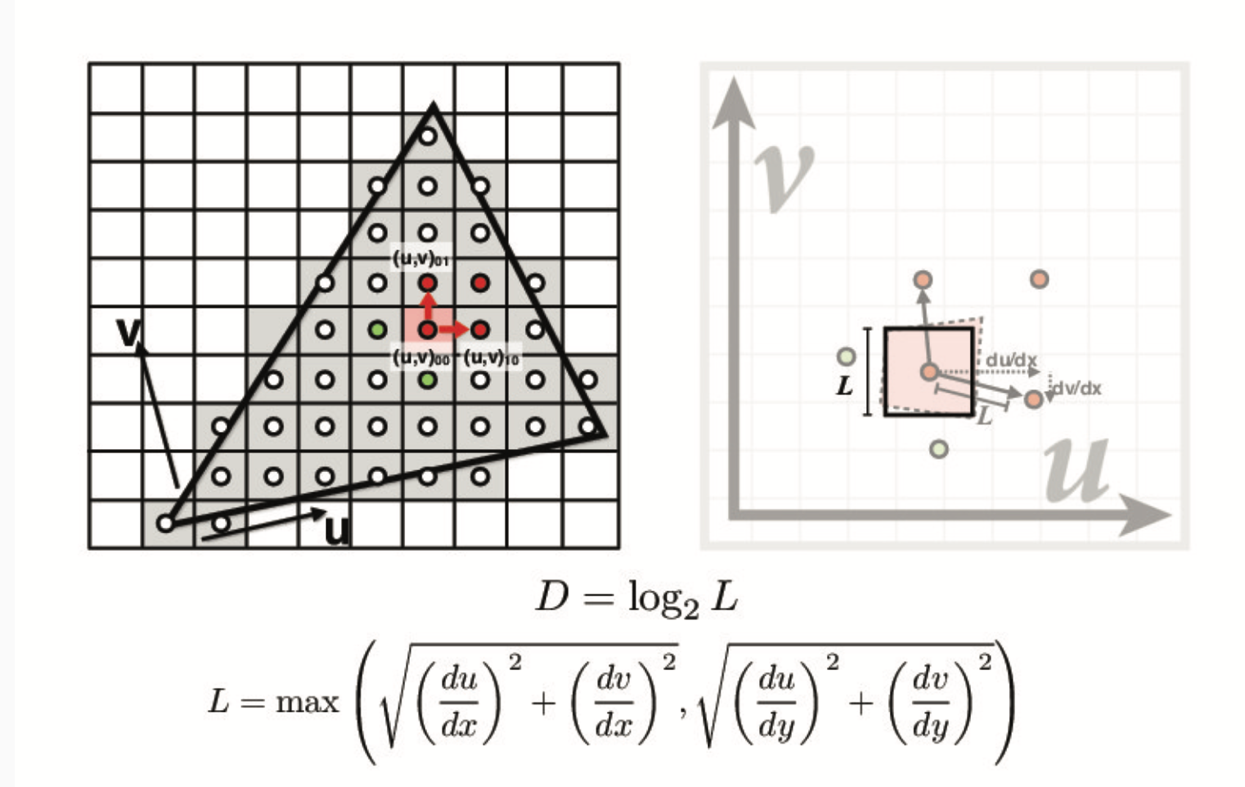
We choose both how we want to resample the image: using either nearest or bilinear interpolation, and how to resample the mipmap level: using level 0, nearest D, or linear interpolation. There are several speed/ memory/ antialiasing tradeoffs when deciding which sampling technique to use:

· Level 0 sampling is memory intensive and subpar antialiasing (does not take advantage of mipmap capabilities)

· Nearest level sampling is less memory intensive than level 0 and performs better for antialiasing, but is not perfect

· Bilinear level sampling has good antialiasing capabilities but is very slow

· Nearest pixel sampling has good rendering speed but poor antialiasing capabilities (as shown before, has lots of discontinuities)

· Bilinear pixel sampling is also slow but performs antialiasing well

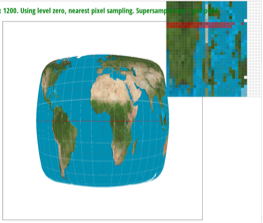
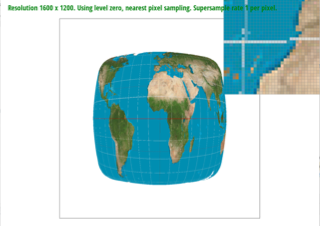
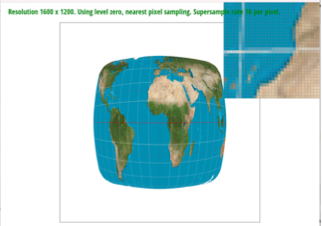
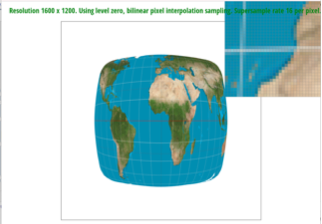
I used an image of Sather Gate to show 4 versions of the image. The outputs show how level sampling methods and pixel sampling methods produce different antialiasing results.

L_ZERO & P_NEAREST	L_ZERO & P_LINEAR
L_NEAREST & P_NEAREST	L_NEAREST & P_LINEAR

CONCLUSION

Overall, this project was both incredibly challenging and rewarding. This project has given me deeper insight into how complex computer graphics is, and how useful linear algebra is! It also made me a better debugger because a single pixel could affect the entire output. Rasterization takes a lot of geometry, linear algebra, and precision.