Task 1: Bezier Curves with 1D de Casteljau Subdivision
In this task, we implemented de Casteljau's algorithm for 1D which is useful for finding Bezier curves.
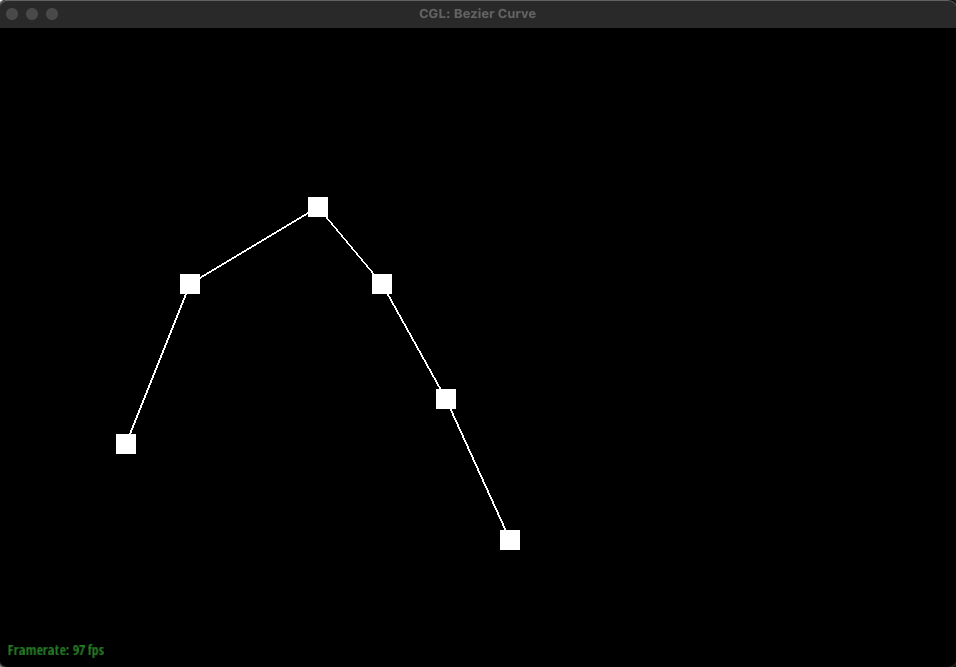
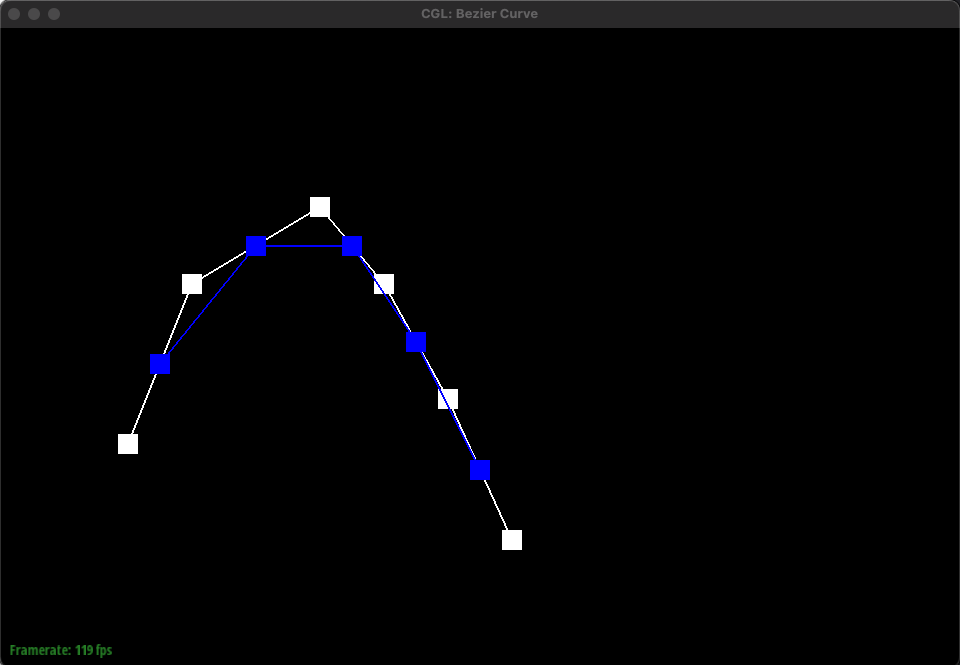
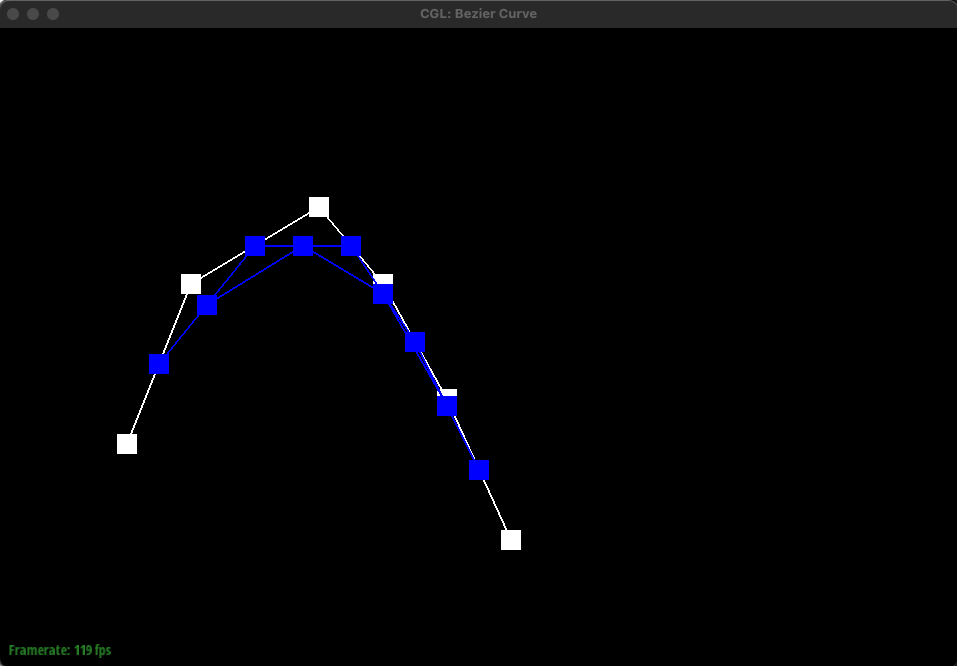
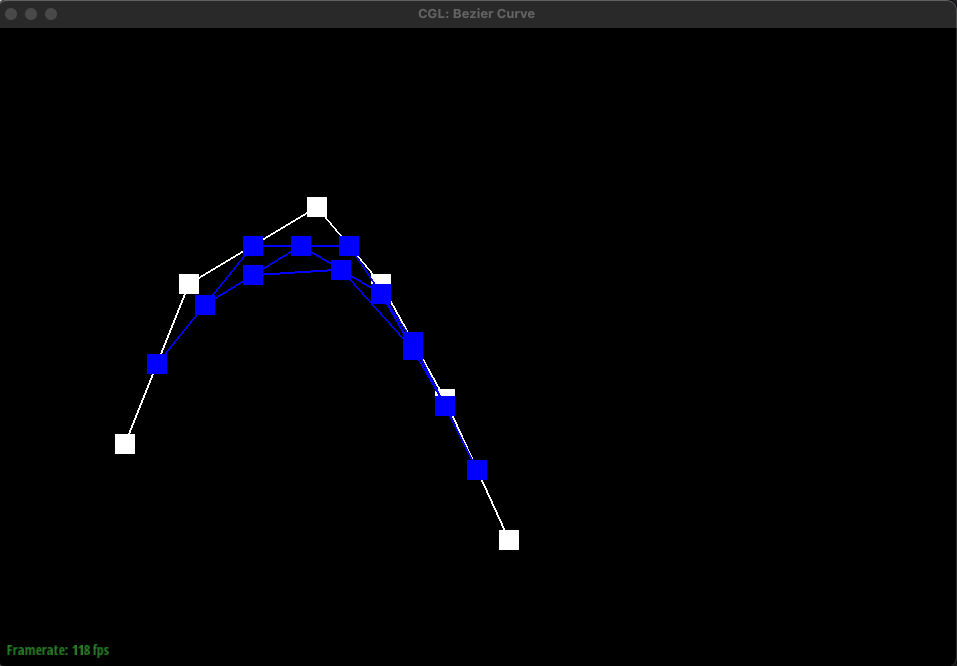
de Casteljau's algorithm takes the given control points, inserts a point using linear interpolation between each control point, and does this recursively until we are left with only one point. Essentially, it recursively finds intermediate control points between each pair of given control points using linear interpolation until only one point remains. This enables for a smooth curve.
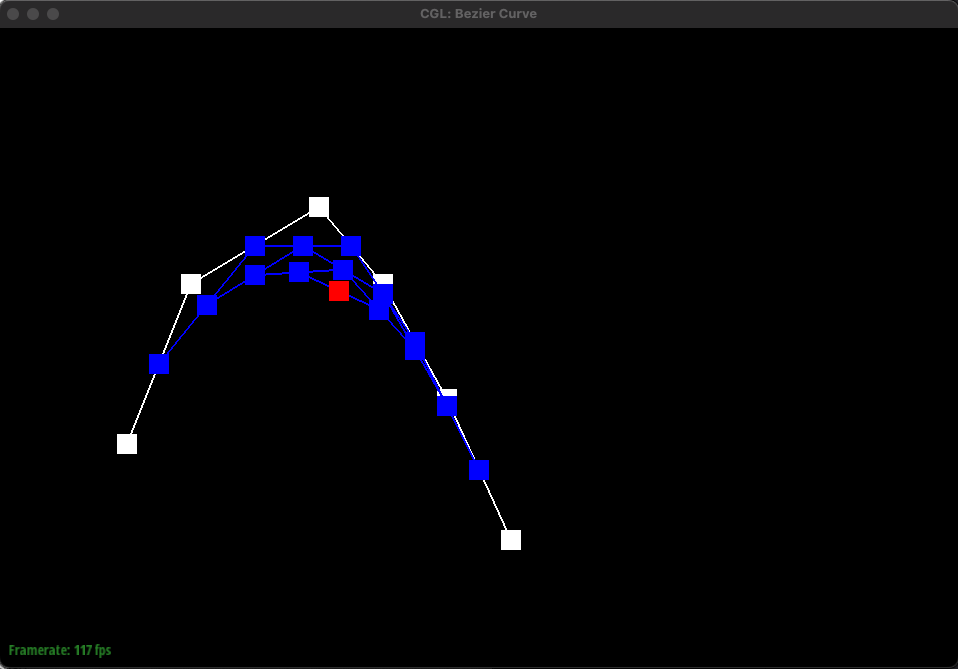
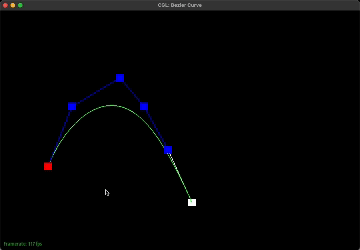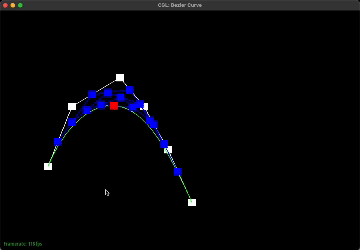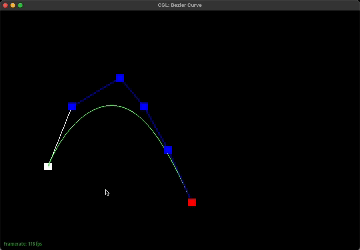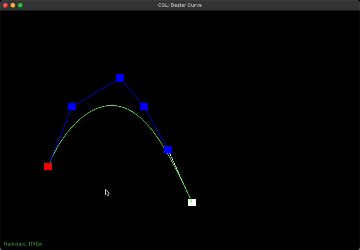
The implementation is straightforward. Simply iterate through the given control points, which is a list of points (x, y) and during the iteration, perform linear interpolation between the current point and the next point and add this interpolated point to a new list of points. This new list containing intermediate points is returned. Eventually, this new list will only contain one final point that lies on the Bezier curve. This final point is the red point shown below in the images.
|
|
|
|
|
|
when parameter t is changed
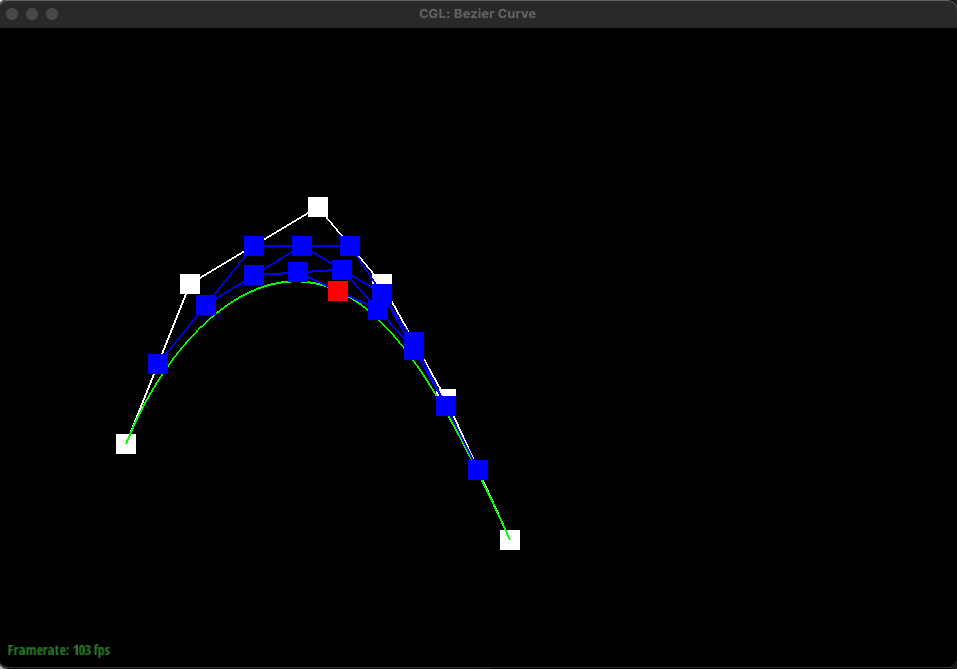
If we have 6 control points, we would have to do linear interpolation 5 times to get 5 intermediate control points for the first step of de Casteljau's algorithm. Then, with these 5 points, we would have to do linear interpolation 4 times to get 4 intermediate points. This repeats until we have one final control point as shown above in the images. Essentially, given n points, we have to find n-1 intermediate points using linear interpolation until we are left with one final point that lies on the Bezier curve. This algorithm is used to find the bezier curve as indicated by the green curve above.
The parameter t ranges from 0 to 1 and determines the position of the final intermediate point. For example, when t = 0, this corresponds to the starting point. In the gif above, it would be the leftmost and bottommost point whereas when t = 1, this corresponds to the last point which is the rightmost and bottommost point. The parameter t essentially controls how far along the curve the interpolated point should be.