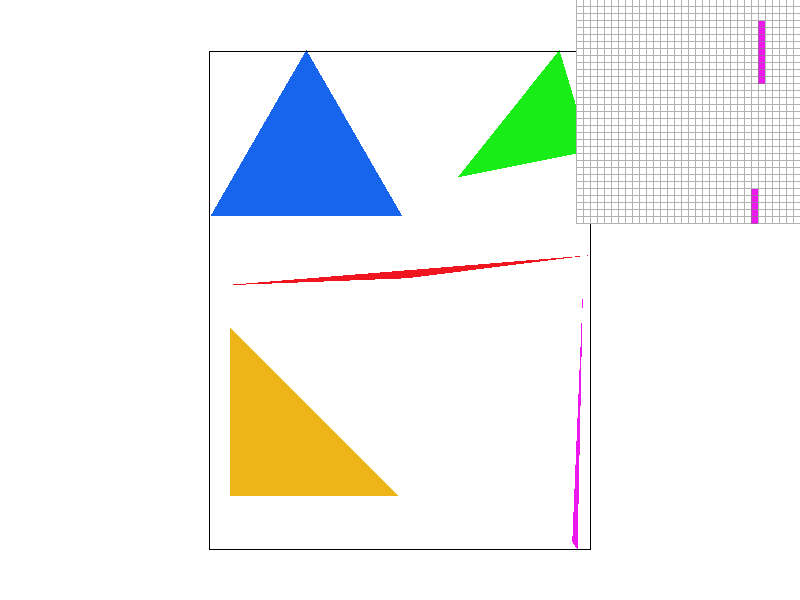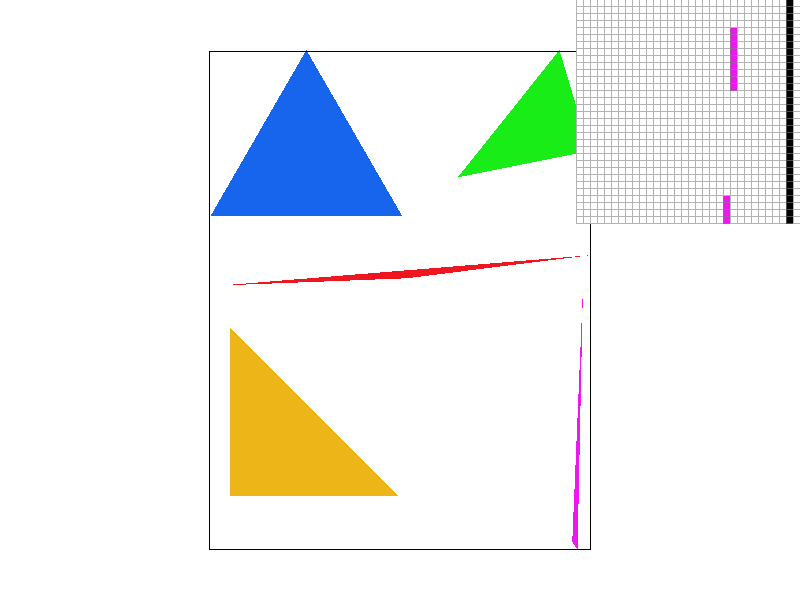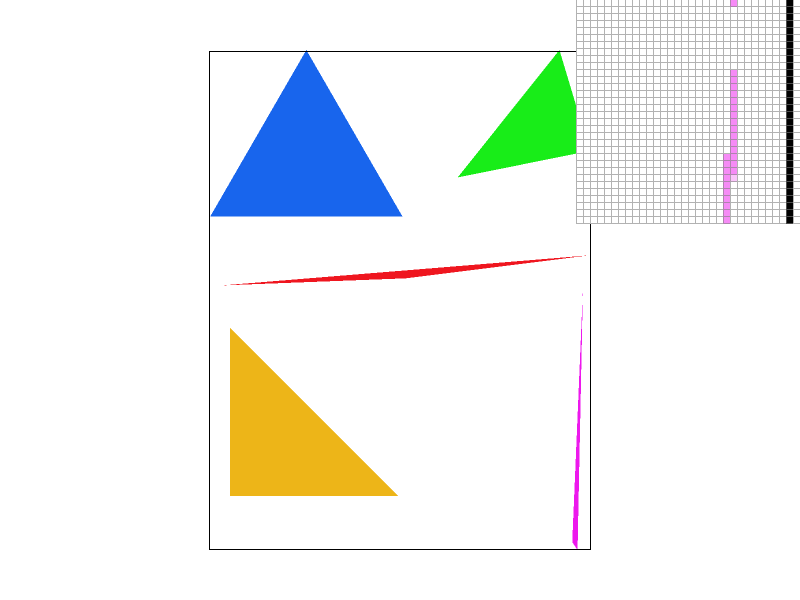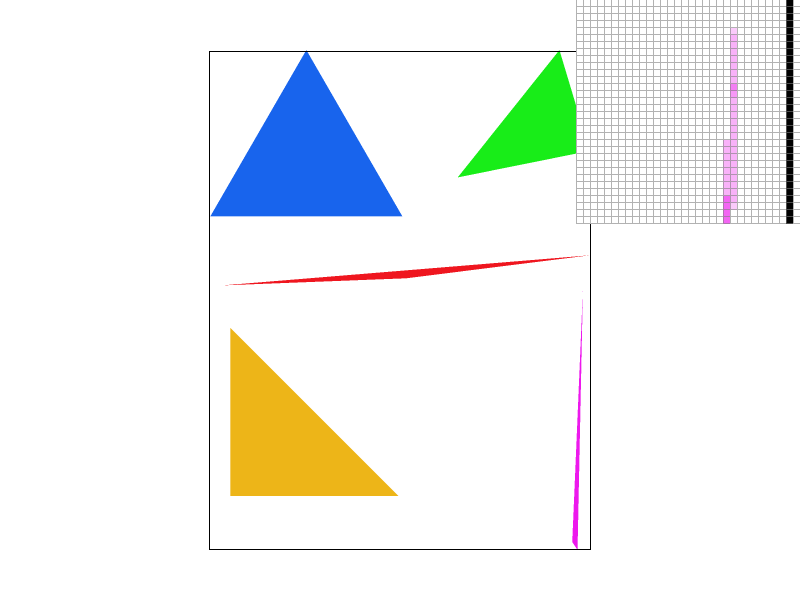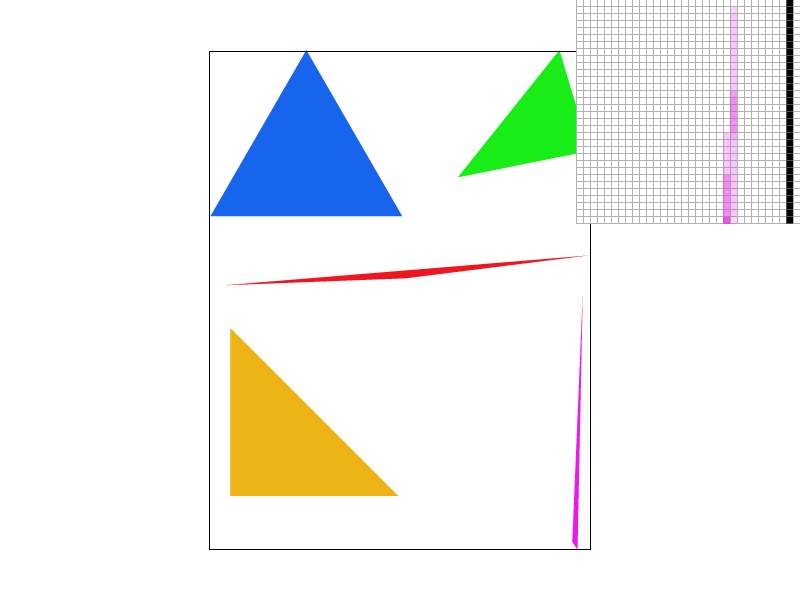In this task, we implemented supersampling to get rid of the "jaggies" that we saw from task 1. In other words, we antialiase by supersampling.

To support supersampling, I had to modify set_sample_rate, set_framebuffer_target, resolve_to_framebuffer, rasterize_triangle, and add a helper function called fill_supersample_pixel.

• `set_sample_rate`

  This function is called when we want to change the supersample rate or when we press = during the runtime of the draw program. The only change needed here to support supersampling is to ensure that when the sample buffer is resized, it is resized to a size of width * height * rate where width and height are the dimensions for the frame buffer while rate is the sample rate. This calculation is needed to support the increased number of samples.

• `set_framebuffer_target`

  This function is called when the draw program window is resized. When the program window is resized, we have to resize the sample buffer as well and to support supersampling, the sample rate is accounted for in the resize calculation.

• `rasterize_triangle`

  Since supersampling is sampling multiple points within each pixel and averaging them, we need to modify this function to have nested for loops in order to iterate over each pixel inside the bounding box. Then, we test these subpixels with the three line test again and if they are within the triangle, we color them using `fill_supersample_pixel`.

• `fill_supersample_pixel`

  This is a helper function I added. This functions similarly to the `fill_pixel` function except it supports supersampling; the function makes it so that all the supersampled pixels, or subpixels, correspond to the pixel in the frame buffer and are changed to the same color. In order to do this, I need to change the way I index into the sample buffer. This is done by accounting for sample rate and keeping track of the sample within the pixel (x, y). This means that I take in one extra parameter which I call `s` and we keep track of it inside the inner loops for the subpixels.

I used the sample_buffer and resized it by doing width * height * sample_rate so that there is enough memory for the subpixels. I also modified the rasterize_triangle function to have two for loops inside the loops for iteration through the pixels. These two inner loops are for iteration through the subpixels; within them, I find the sample point for each subpixel. Then, I perform the 3 point test and if it passes, I call on fill_supersample_pixel to fill the subpixel with the specified color. I also keep track of the index of the current subpixel so that in fill_supersample_pixel, I can index into the correct sample_buffer. The function resolve_to_framebuffer is also modified by taking our subpixels and averaging them down.

As supersampling rate increases, the triangle edges are smoother. This is because supersampling is essentially taking a higher resolution and then downsampling and averaging it to the output resolution of the frame buffer.

In this task, we have to implement three transforms: translating, scaling, and rotating. These transforms utilize a 3x3 matrix for homogeneous coordinates.

In this task, we have to implement rasterizing a triangle with colors defined at the vertices and interpolate the pixel colors using barycentric coordinates.

Barycentric coordinates is basically a proportion between a point inside a triangle and the triangle's vertices. The way I think about barycentric coordinates is to imagine the triangle as a physical object with mass distributed at its three vertices. This way, the point given by barycentric coordinates, or the point inside the triangle, would be the center of mass. In other words, barycentric coordinates ensure that the point inside the triangle is the center of mass of the triangle. This is why barycentric coordinates consist of three scalar values: alpha, beta, and gamma representing the "weights".

This implementation is similar to `rasterize_triangle` except that once we are in the innermost loop and after finding the sample points as well as performing the three line test, we calculate alpha, beta, and gamma based on the formula in lecture. We then use these alpha, beta, and gamma values to find the center of mass which would be the color that we want our `fill_supersample_pixel` to use.

In this task, we have to implement pixel sampling using two methods: nearest neighbor or bilinear interpolation.

Pixel sampling is when you apply a texture into screen space. You take a pixel and its corresponding color from the texture and map it to the pixel in screen space. This requires the color information, ie where it is located in texture space, from the texture to determine the final color of a pixel. To do this, I had to find the barycentric coordinates (alpha, beta, and gamma) of the sample point. After this, I have to convert to the sample point to texture space by using these alpha, beta, and gamma values. Once the sample point is converted to texture space which is represented by (u, v) coordinates, we then apply texture sampling using either nearest neighbor or billinear interpolation method.

In nearest neighbor sampling, we simply take the closest (u, v) coordinate and sample the texture at that point. On the other hand, in bilinear interpolation, we get the four closest (u, v) coordinates and then do a weighted average (through linear interpolation) and then sample.

The following functions were implemented for pixel sampling:

• `rasterize_textured_triangle`

  This function is very similar to the other rasterize triangle functions except it converts to (u, v) coordinates. These coordinates are passed onto the `sample` function.

• `sample`

  This function returns the color for the pixel from the texture based on the pixel sampling method.

• `sample_nearest`

  This function takes the nearest texture coordinates and returns the color. This is done by taking the (u, v) coordinates to match the width and height of the mipmap level, which is always 0, for pixel sampling.

• `sample_bilinear`

  This function takes the nearest four texture coordinates and returns the interpolated color. We also have to scale the (u, v) coordinates to match the width and height of the mipmap level.

Between nearest sampling at supersample rate 1 and bilinear interpolation at supersample rate 1, we see that the latitude lines (horizontal white lines) are a bit more blurry or better antialiased for bilinear interpolation.

Then, for the methods with supersampling rate 16, the differences are much harder to tell because supersampling already antialiases; however, bilinear interpolation is still better. For example, if you look at some of the longitude lines closely, it is a bit more blurry.

With these observations, there will be large differences when the supersample rate is at 1, or when there is no supersampling. Nearest sampling tends to produce blocky, pixelated, and sometimes jagged edges since it only takes the nearest texel and not consider other adjacent texels like bilinear interpolation does. This is especially noticeable when we zoom in with the pixel inspector at pixels where we move from high frequencies to low frequencies.

Looking at the pixel inspectors, we can see how bilinear interpolation is much better when going from high frequencies to low frequencies. In this case, from the black pixels to the brownish/lighter pixels.

In this task, we have to implement level sampling to the pixel sampling algorithm from task 5.

Level sampling works by sampling from different levels, or resolutions. These different resolutions are stored in a something called a mipmap. We use the mipmap to sample at lower resolution for higher frequencies.

• `rasterize_textured_triangle`

  I implemented level sampling by additionally finding the barycentric coordinates for the sample point's neighbors. These neighbor barycentric coordinates are used to calculate the level in the `get_level` function. These neighbor barycentric coordinates are first used to find the rate of change of u and v in respect to x and y respectively. This is so that we know which level in the mipmap to use. Larger derivatives result in larger level values and therefore lower resolutions. This is implemented in `get_level`.

• `get_level`

  We use the derivatives mentioned above and using the level calculation in lecture to find the level.

• `sample`

  Once we find which level to sample from, we can either use the two methods from before: nearest or bilinear interpolation. With nearest level, L_NEAREST, we use the nearest level to sample from. With L_LINEAR, we take two levels above and below the level returned by `get_level` and interpolate them.

With level sampling implemented, we can have in total 3 level sampling methods and 2 pixel sampling methods.

With everything implemented, we can discuss the tradeoffs between speed, memory usage, and antialiasing power between supersampling, pixel sampling, and level sampling. Supersampling is a powerful antialising technique; however, it requires more memory to store the higher resolution image. It is also computationally more intensive due to the number of increased number of samples per pixel. Pixel sampling is not as effective compared to supersampling especially for high frequency pixels. It sacrifices some antialiasing power. Because of this and because it does not sample subpixels, it requires less computational power and no additional memory. Level sampling antialiasing power is more of a balance of supersampling and pixel sampling in that it precomputes multiple texture resolutions and stores them in a mipmap and utilizes them to reduce aliasing across different viewing distances. Therefore, it is better aliasing power without having to worry about needing more computational power at the expense of requiring additional memory for the mipmap.