Title: No rest for the liquid

Team Members: David Ban, Jackie Dai, Hailey Tran, Jesse Lutan

Youtube Link: https://youtu.be/1dpUuDcknkU

Abstract

Fluid simulation is an already well-discussed problem. To expand on this increasingly-complex topic, this project aims to create a video game that will be able to realistically render water in real time that will react to various forces over time. The player will be able to place objects that can then interact with the water in a three dimensional way. Rather than focusing solely on accuracy of fluid simulation, we hope to cut down and optimize specific steps in order to have a real-time simulation for our game.

Technical Approach

The main aspect of this game is obviously the fluid simulation. To generate this, we used a Forward-Euler simulation of particles. The environment was created from scratch in Unity, and utilizes the computer’s GPU to speed up the process.

Each Particle contains 5 descriptors: Pressure, Density, Current Force, Velocity, and Position. With these, we are able to predict approximately where the particle will be in the next time step, along with how it affects other particles. One of the key benefits of working in Unity is that we are able to edit and save hyperparameters such viscosity constants, particle masses, without long build times.

Particle Simulation

Following the steps of Müller [1], we model fluids with particles based on a particles pressure and viscosity. While the paper does also include surface tension, we decided that it would not impact our model enough to warrant the computational cost on the GPU, since real time was more important to us than complete accuracy. However, as mentioned in class during the physical simulation lecture, Forward-Euler can lead to unstable results due to accumulating errors. To that end, we also implemented the several suggested smoothing kernels that build off of the Smoothed Particles Hydrodynamics (SPH) and applies it to fluid. The smoothing kernels are described below.

General Kernel

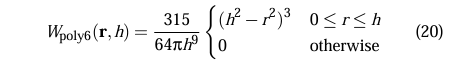
Used for the general case of density, where h is the core radius, and r is the difference in particle position.

Spiky Kernel

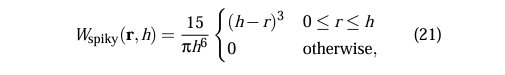
A spiky kernel is used for the computation of pressure forces. This is needed because pressured particles tend to clump up tightly, meaning little (but non-zero) repulsion should be applied. The general smoothing kernel doesn’t reflect this behavior.

Viscosity Kernel

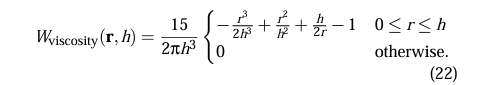
A kernel that is used for the computation of viscosity forces. This kernel fixes the general smoothing kernel’s issue with negative values resulting from its Laplacian.

Object Collision

Since we are aiming to have interactivity within our fluid simulations, the particles must interact with other objects and not itself and its neighboring particles. This took much of our brain power, and coding the interaction of particles with non-spherical objects caused many headaches.

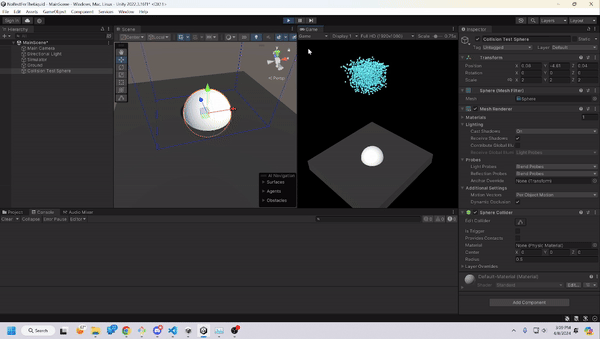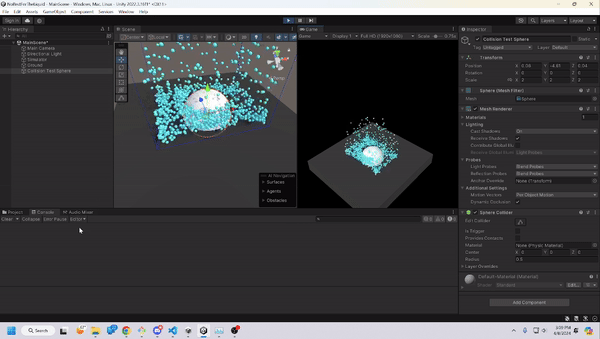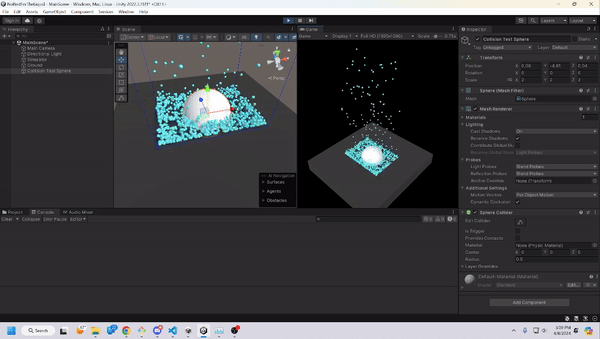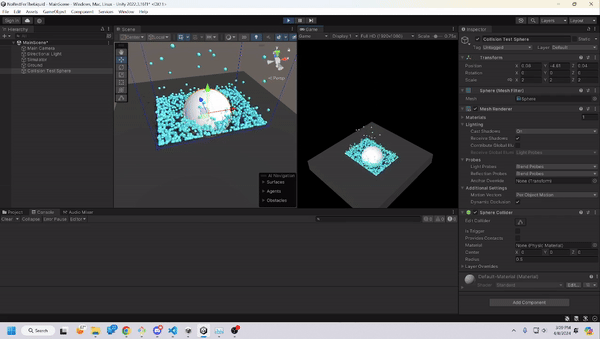
Spherical Collisions

Spherical collisions were very similar to the mesh project, as we had to see if any of the particles are within the radius of the sphere. If so, we need to push them out. Nothing out of the ordinary.

Cubic Collisions

Cubic collisions required much more thought than spherical, as it requires more than one check. Furthermore, we wanted to generalize the collision boxes to include all three axes of rotation as well.

This meant implementing the rotational matrix from lecture, along with defining the faces of the cube through plane definitions (a point and a normal vector). This also meant that we would be converting between two different axes, one for the world, and one for the cube. With this information, we can then check if a point is inside of the cube, and then from there determine where to push the vector. We would also have to reflect the velocity as it exits, which was very similar to the light reflection we implemented from the ray reflection.

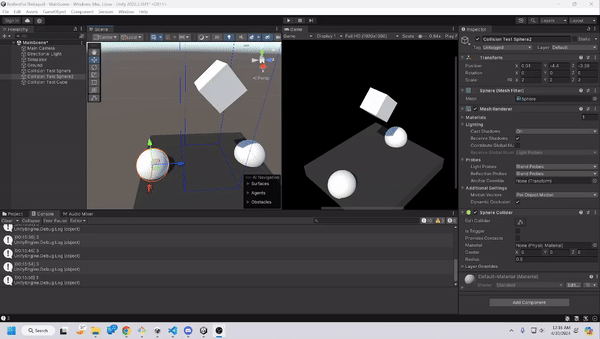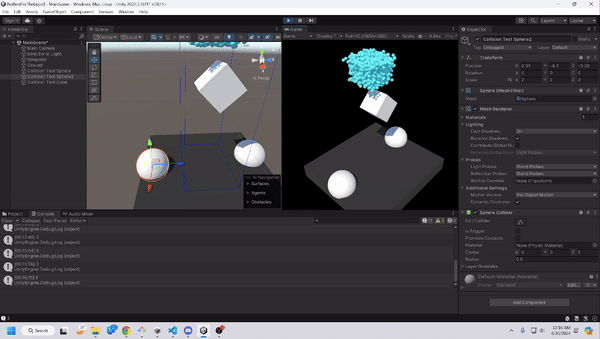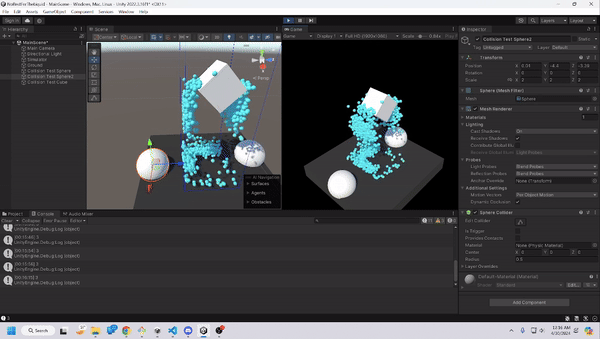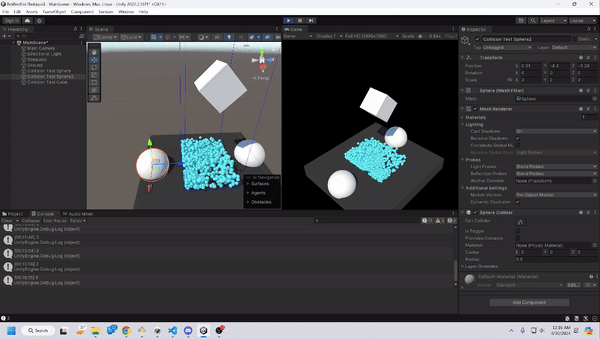
Liquid Shader

As stated before, we weren’t looking for the most realistic water, and thus decided to just go with a constant colored water much like the water in Where’s My Water. To do this, we utilized RayMarching and Smooth-minimums to create a believable liquid without having to worry about complex shading and long rendering times.

Raymarching

Raymarching is a rendering technique used by tracing rays, much like our project. However, unlike traditional rendering methods, it does not rely on predetermined equations for geometry. Instead, it iteratively “marches” along the ray and determines if a ray intersects with objects in the scene. This allows us to render complex shapes with relatively simple code, which is necessary for smooth-minimums.

SDFs allow us to return the shortest distance between a point and some surface, with the sign of the returned value indicating whether the point is inside or outside of the surface. Although trivial for objects such as spheres, it can get complex with other objects - luckily, for this project, we are only concerned about spheres. With this, we are able to determine which object is the closest from the point we are on along ray. We then increment that distance along the ray, and repeat until the ray collides with the object.

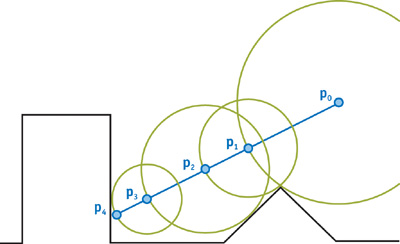
Example 2D Raymarching [2]. Each p value indicates another step, with the green circles demonstrating the closest intersection at each step.

Smooth-minimums

Smooth-minimums allow us to find the minimum value between functions in a smooth and continuous manner. This is employed in our case to create transitions between particles in the scene, which will function as our “liquid”, since it removes the jagged and rough lines. By integrating smooth-minimums into our distance functions in raymarching, we can create smoothly blended liquid, that react like liquid particles. There are many different kinds of smooth-minimums, but we decided to just go with a polynomial approach as that was the easiest to implement.

Example Smoothed Minimum between a rectangle and a sphere. Notice how they smoothly connect between each other and is always within the span of their respective BVH denoted in light blue.

Using raymarching as our rendering method, and smooth-mins to create generally believable liquid, we end up with this outcome, which was to our satisfaction. We do admit that it could look more realistic, either through a more detailed shader, or with more particles, but as mentioned earlier, our priority was that the game could run smoothly on a laptop with GPU, rather than aim to be the most accurate liquid model.

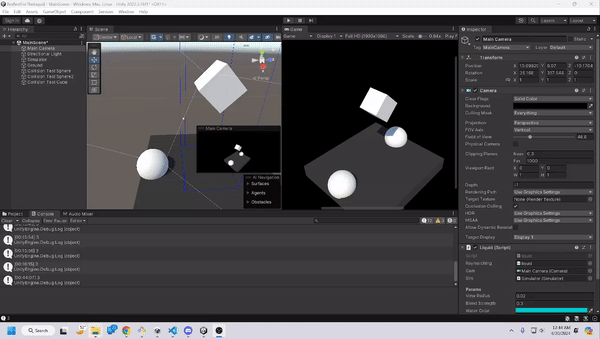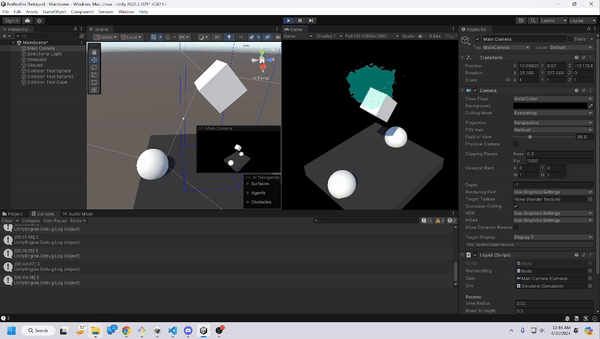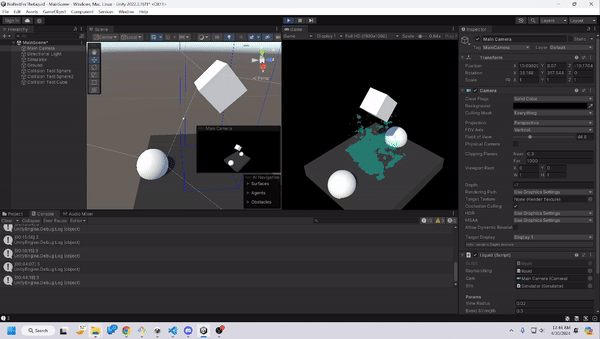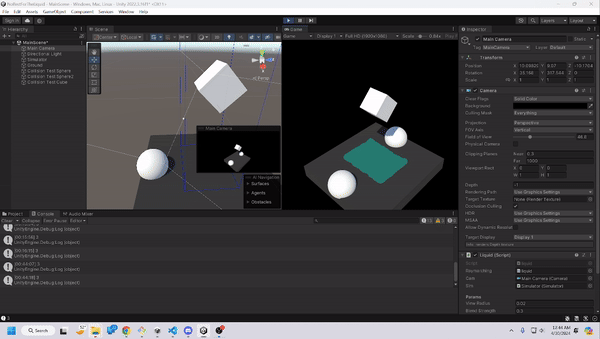
Bounding Boxes

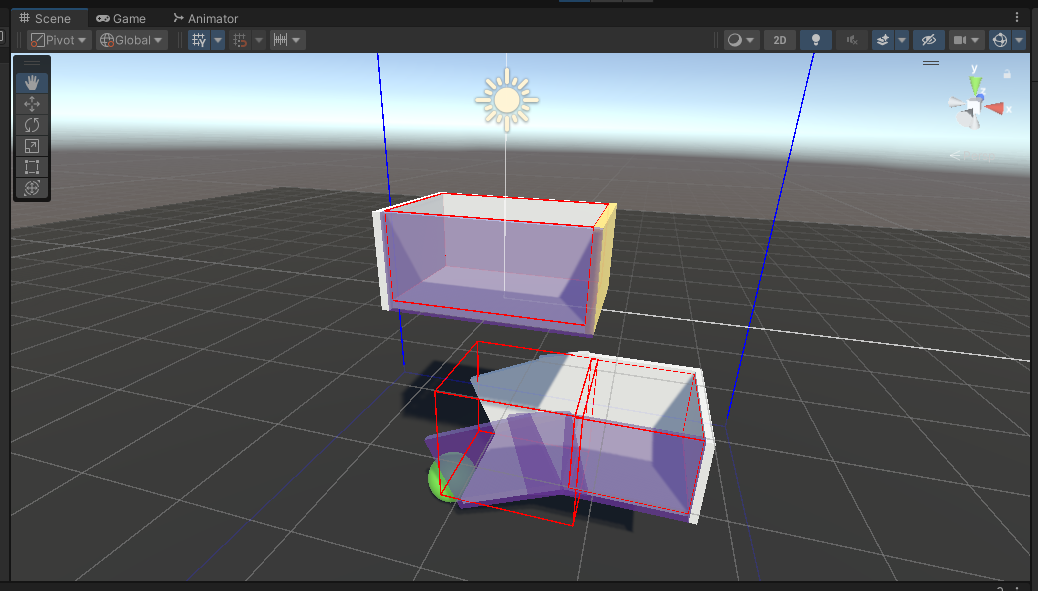
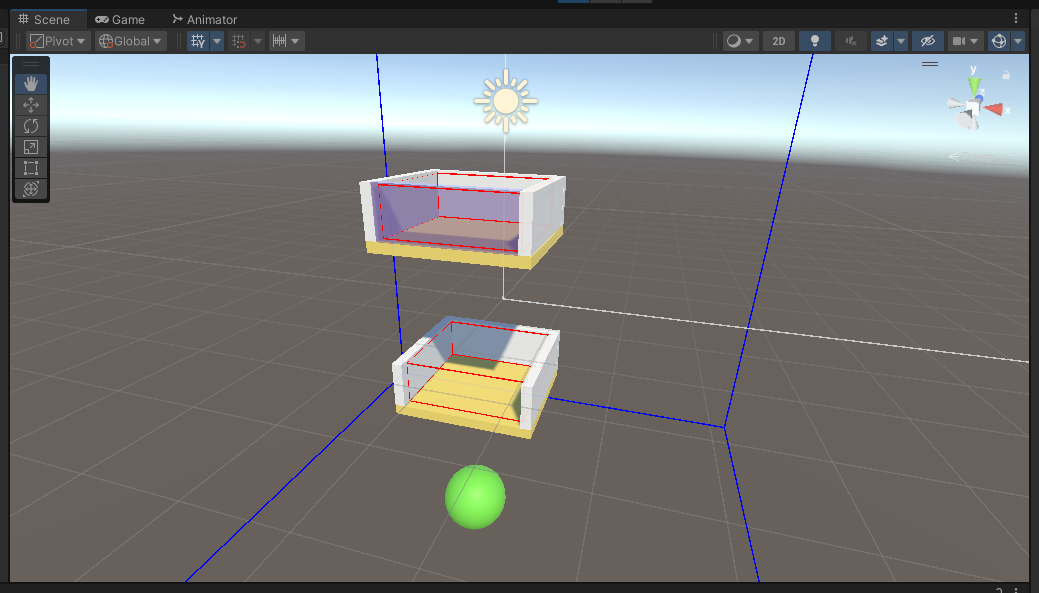
To implement the bounding box functionality, we first had to set the proper dimensions based on each type of obstacle. For the 2 obstacles in level 1, we were able to generalize the code to automatically compute the bounding box’s position and size, based on the actual model! We made 3 different types in total: the holder_right, platform, and holder_bottom.

Then we took 2 corner points and compared it to the particles’ position. If the particle was inside the bounding box, we’d check whether not the obstacle’s gate was open or closed and re/deactivate the corresponding face.

Results

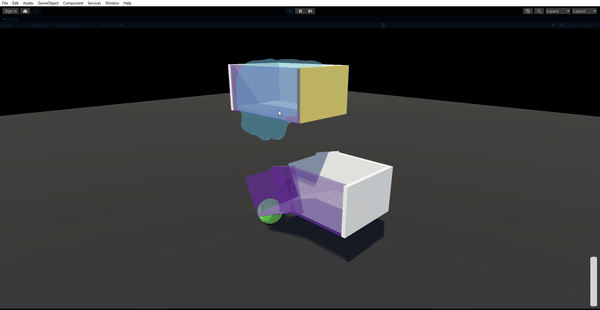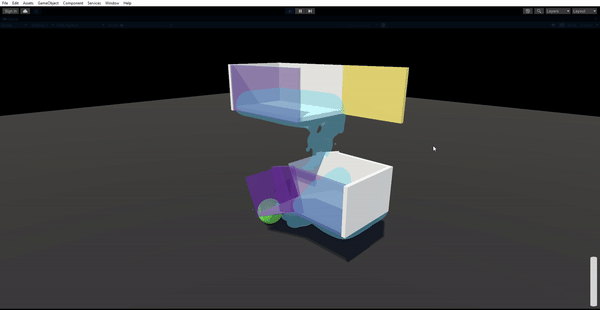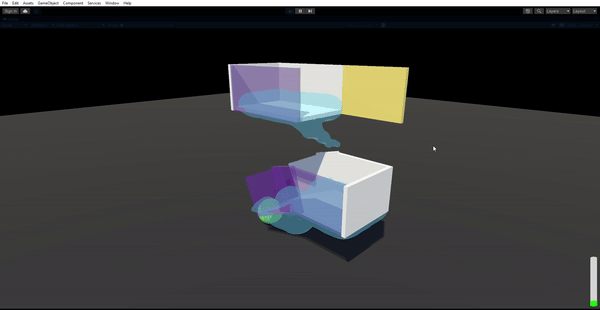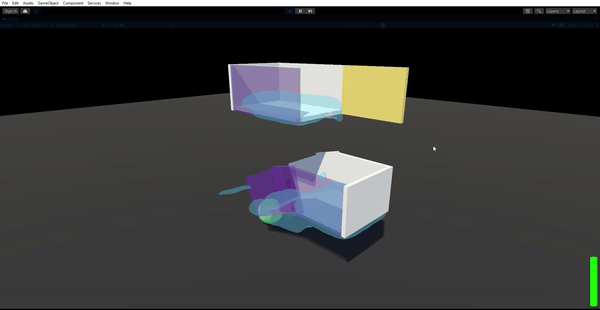
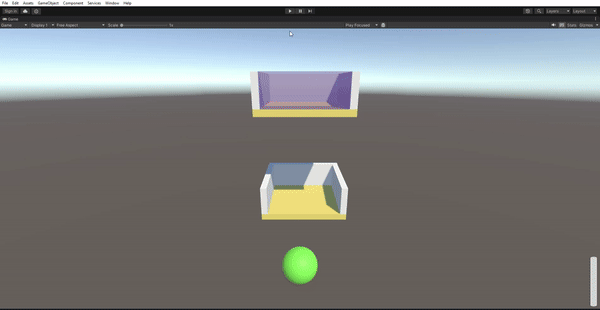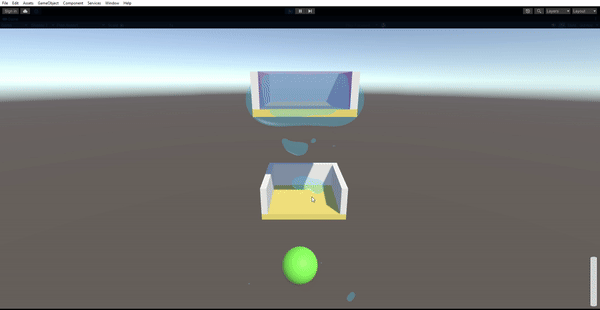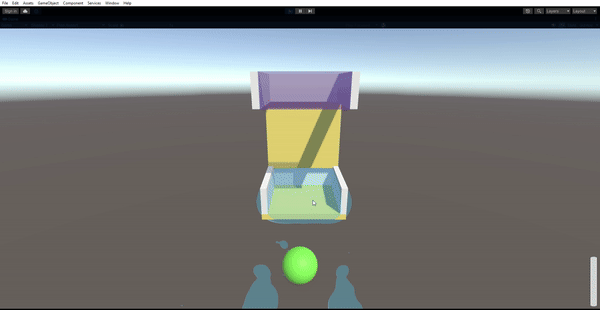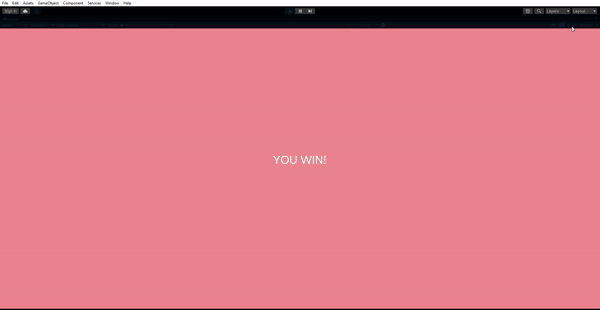
Lessons Learned

Using a totally different framework than what we implemented in class definitely increased the initial learning curve, but we found it easier to work with as we got to know the structure of Unity more - specifically the shader side of it. Furthermore, we learned that in order to render models in real time, there has to be a lot of trade offs based on the level of detail, even with GPU acceleration and trying to implement more efficient algorithms. Like the mesh project, it was extremely important to maintain numerical stability of the physical side between the particles for a realistic result.

Collision handling was also much harder to implement than we expected. What we thought would only take a day ended up taking basically an entire week to get right - and even by our final deliverable, definitely could have been better. For non-normal shapes, it’s extremely difficult to calculate forward-Euler simulations as calculating the normal vector and the necessary reflection of velocities varied at each angle.

Division of Tasks

David

• Implemented the physical basis of the liquid simulation
  • Allowed for the ability to use GPU to accelerate the calculations needed for liquid sim in Unity.
  • Implemented math for all smoothing kernels and physical properties (density, pressure, viscosity)

• Implemented collision with other objects
  • Sphere collision
  • Cube Collision

• Handled all liquid raytracing including all of raymarching and smooth-min implementations.

Hailey

• Created the custom 3D models and animations (gate mechanic and static platform)

• Created bounding boxes for containers to handle collisions
  • Activated/deactivated bounding box faces depending on the position of the particles to allow water to pass through or be blocked

• Added support for nested obstacle game objects

Jackie

• Implemented demo level

• Implemented level 1 and 2

• Work with water/particle collisions with sphere to fill water gauge

• Implement reset button

Jesse

• Parts of presentation

• Main menu and level selector

• Icon

Works Cited

[1] “Particle-Based Fluid Simulation for Interactive Applications” https://matthias-research.github.io/pages/publications/sca03.pdf

[2] Raymarching image https://developer.nvidia.com/gpugems/gpugems2/part-i-geometric-complexity/chapter-8-pixel-displacement-mapping-distance-functions

[3] Raymarching algorithm explanation https://jamie-wong.com/2016/07/15/ray-marching-signed-distance-functions/#the-raymarching-algorithm

[4] Smooth Minimums https://iquilezles.org/articles/smin/