Homework 2: Mesh Edit

David Ban

Sp 2024

Overview

This project aims to go over the fundamental topics of geometric modeling, including Bezier curves and half edge data structures. These implementations included mesh operations such as edge manipulations (such as flips and splits) along with subdivision.

Task 1

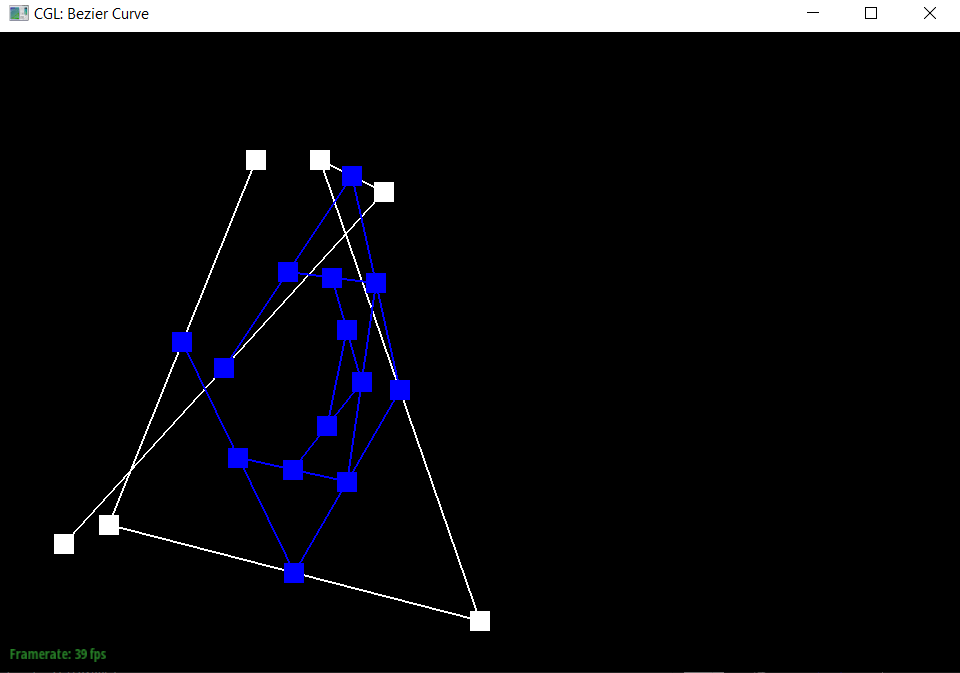
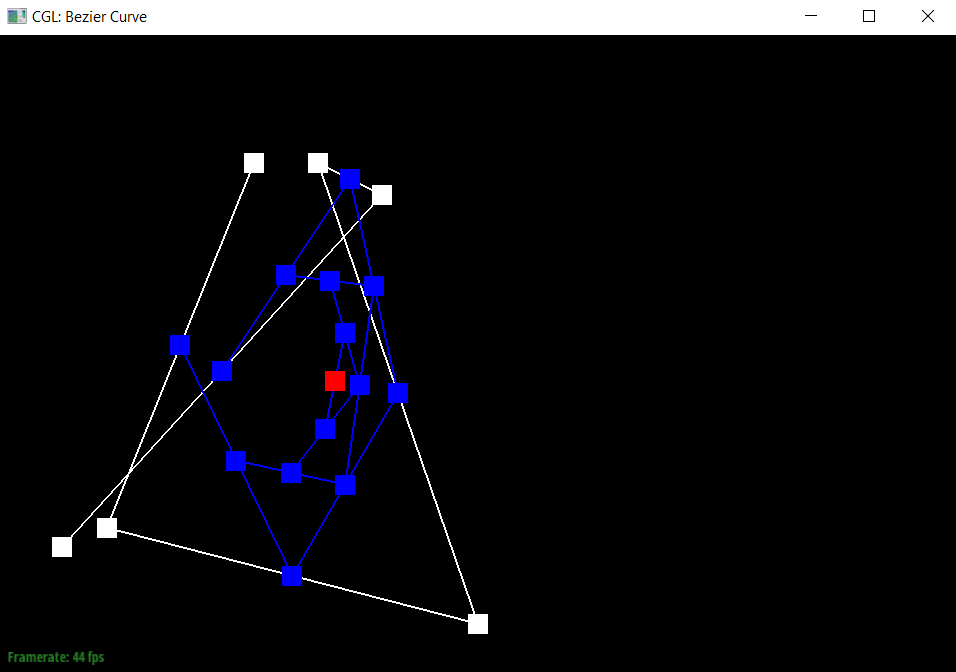
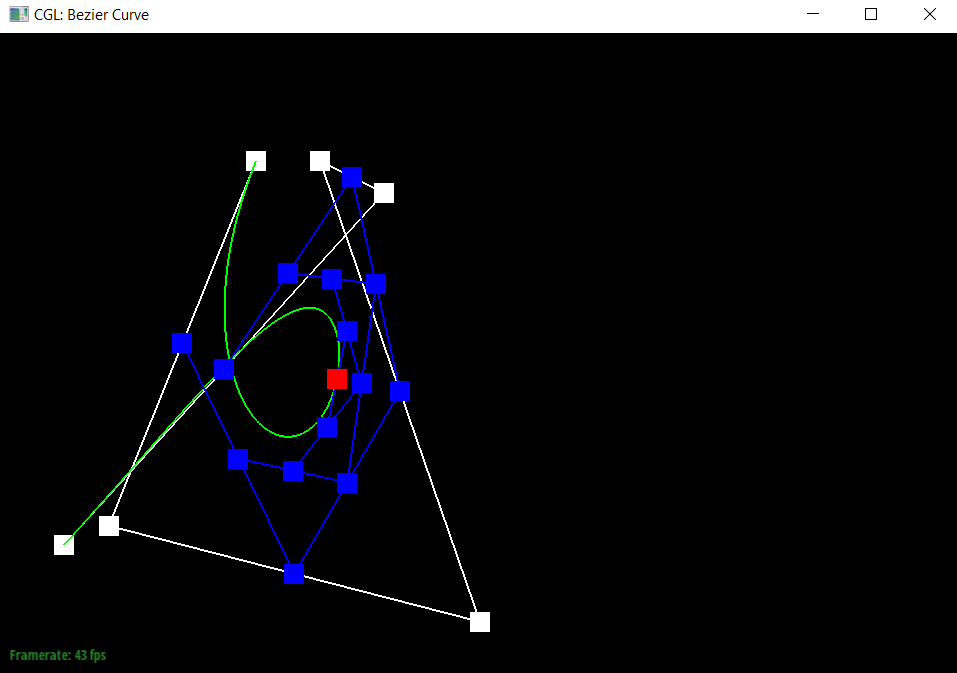
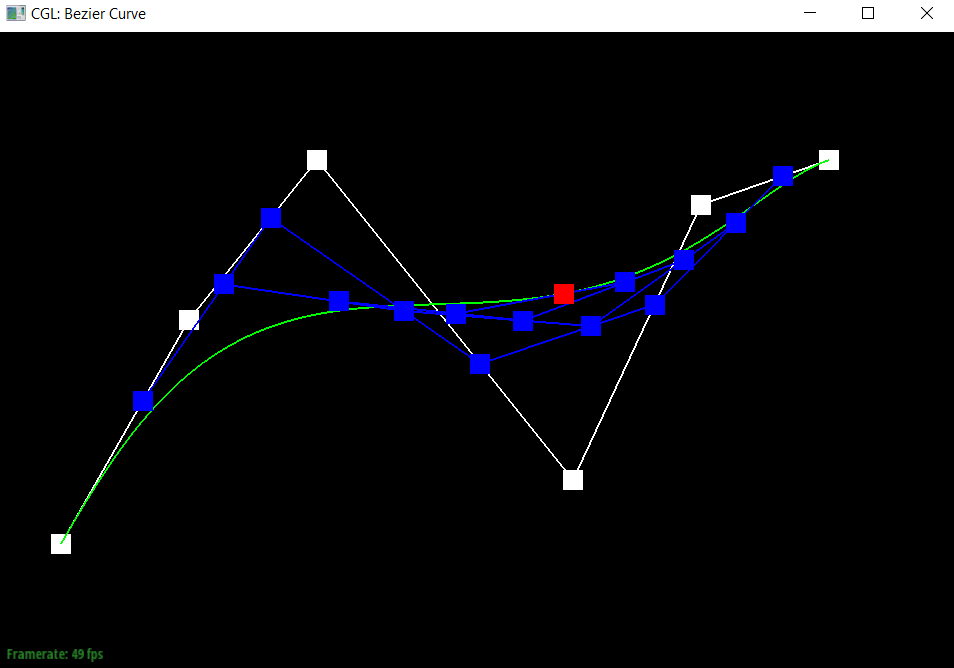
To generate Bezier curves, I added the de Casteljau’s algorithm, which would apply linear interpolation n-1 times (once for each pair of connected points) for a step when there are n points, and return us new n-1 control points. We could then apply this until there is only one point left, which would become a point on the Bezier curve.

Level 0	Level 1
Level 2	Level 3
Level 4	Level 5
Completed Curve	Modified t-value and shifted points

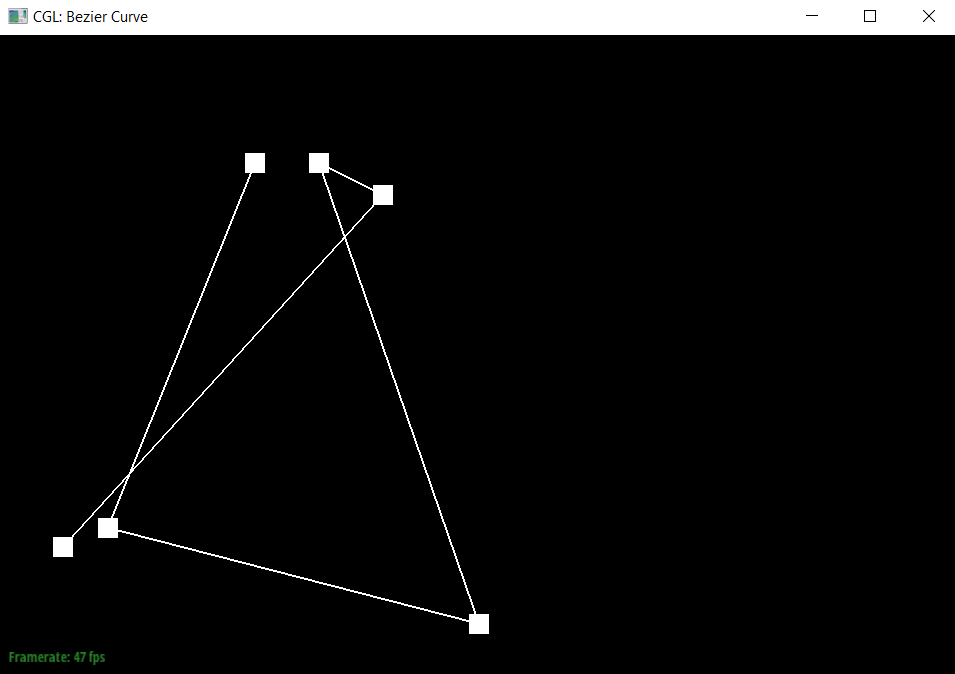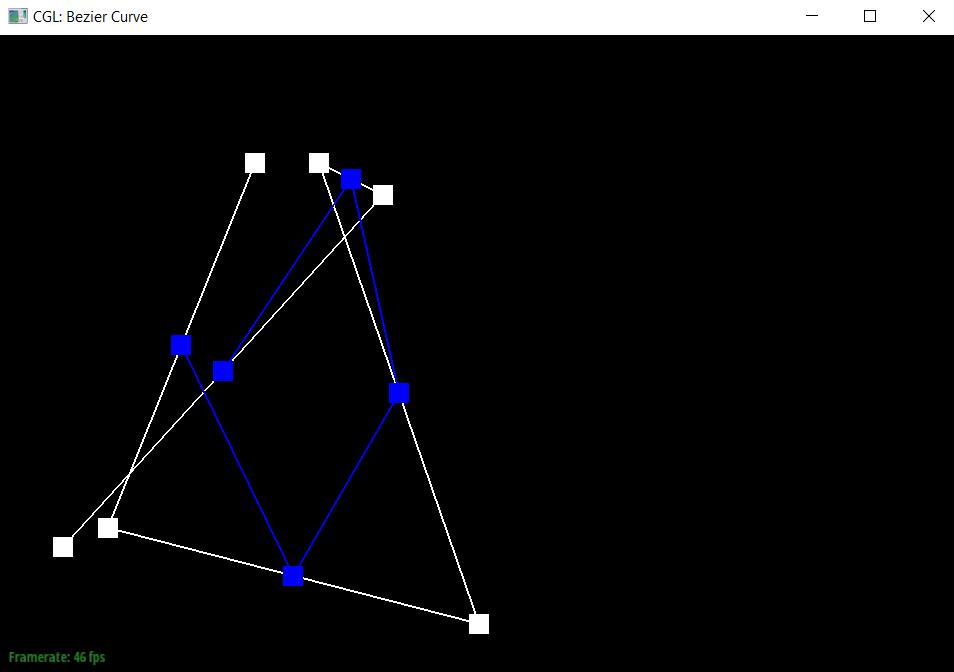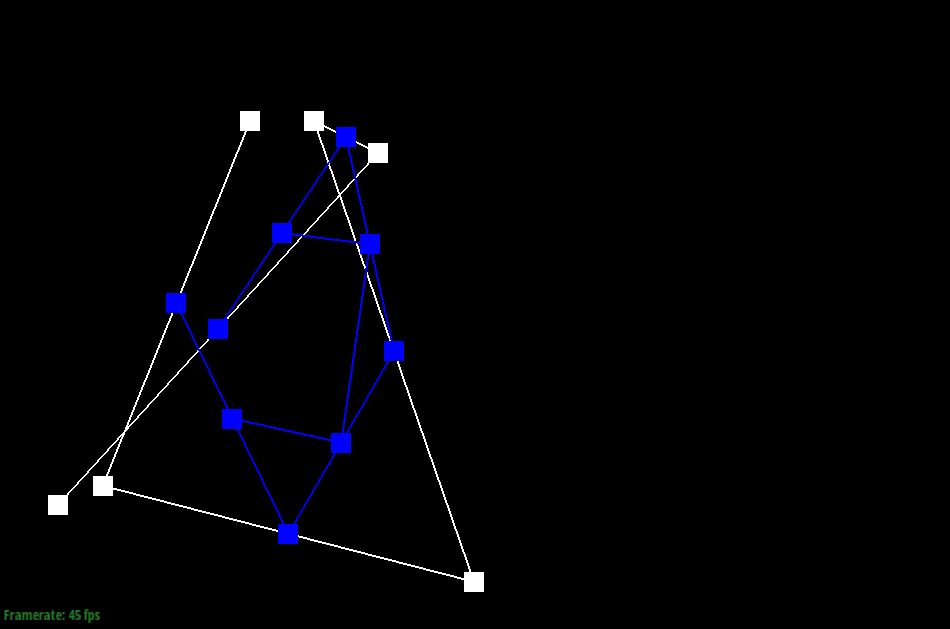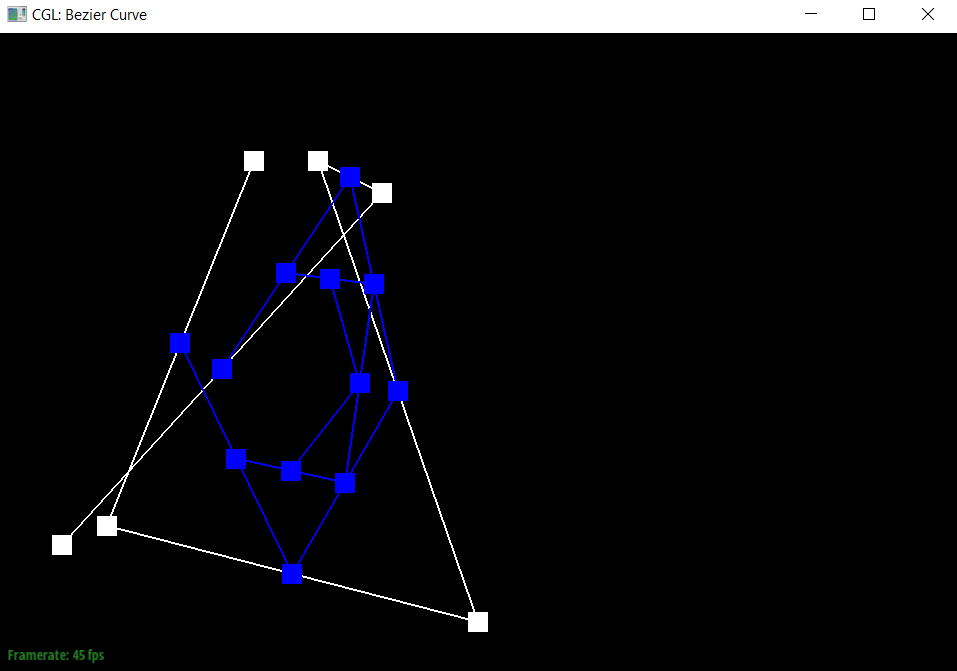Task 2

In order to evaluate Bezier surfaces, I edited 3 functions. You can extend Task 1 to here, by just turning it into 3d - the concept remains the same.

• evaluateStep(): This is the same as the previous task, except now in 3 dimensions instead of 2. It still uses de Casteljau’s algorithm and calculates the next step.
• evaluate1D(): Recursively call evaluateStep() on the list of 3D points until one point remains, which it will then return
• evaluate(): This will first iterate through each row of the initial 2D array of control points, and then evaluate them at their u position using the evaluate1D function, and then adding that point into a new list of points. After that, we can run evaluate1D on the list of new points to return the final surface point.

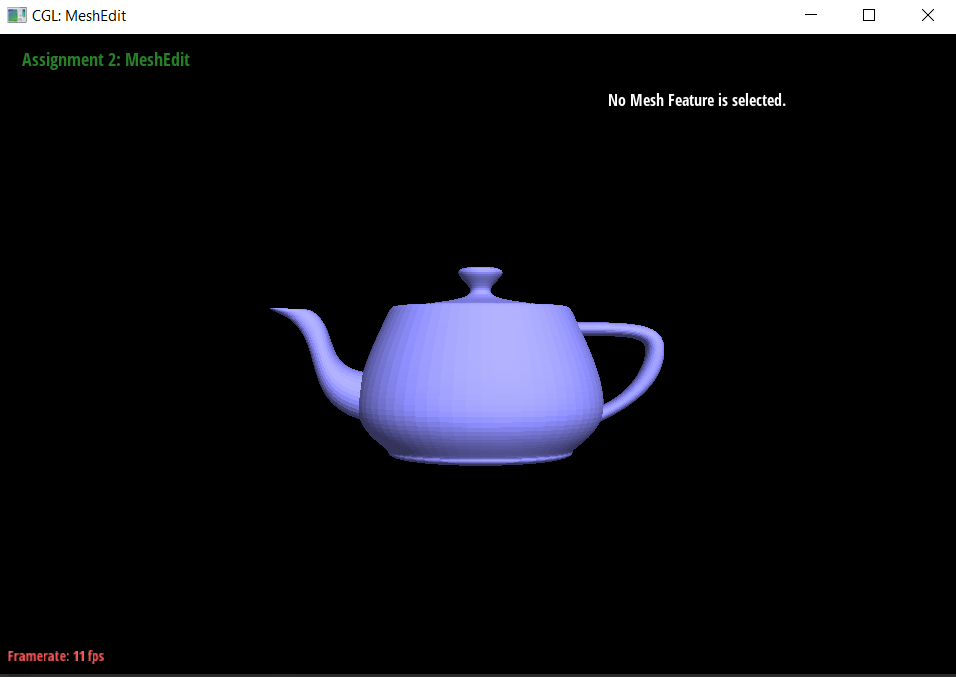peep that 11 framerate though

Task 3

To compute the area weighted vertex norms, I iterated through the halfedges to get to every face that is connected to the given vertex. Then, for each face, I computed the area weighted normal by using the orthogonal vector, and weighted it by the normal. I then added all of these weighted normals, then normalized the final vector to give us the approximate unit normal.

|

Teapot with Flat Shading| Teapot with Phong Shading| |–|–|

Task 4

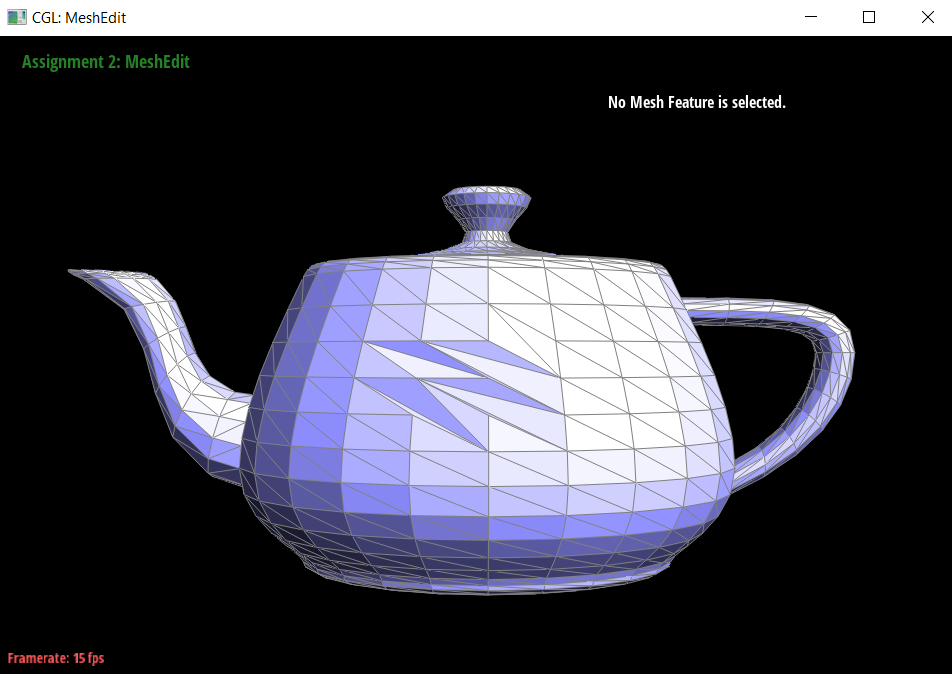
I implemented the edge flip operation by storing every single pointer to each halfedge, edge, face, and vertex of the initial triangle. Then, I updated the pointers (after many hairs were pulled out).

• This was particularly hard for me just because it was difficult for me to totally visualize the entire edge flip. I had to draw it out (in code), which I’ve shown below. ``` c c h1 | h5 h2 h0 h1 a h0|h3 d a d | h4 h3 h5 h2 b h4 b

```

|

Regular teapot| Teapot with edge flips| |–|–|

Task 5

To do an edge split, I moved the initial splitting edge such that it becomes 3 additional edges. I then, similarly to Task 5, saved all of the edges, half edges, etc, and then added the extra parts as well. Finally, at the very end, I changed the pointers to have the correct orientation.

• A tip that I kept to keep myself sane is that I checked to make sure how many extra edges I needed, and if that checked out in my code. And if so, which edges correlated to each one. This was much simpler after the headache that was task 4 for me.

|

Regular teapot| Teapot with edge splits| |–|–|

|

Regular teapot| Teapot with edge flips and edge swips| |–|–|

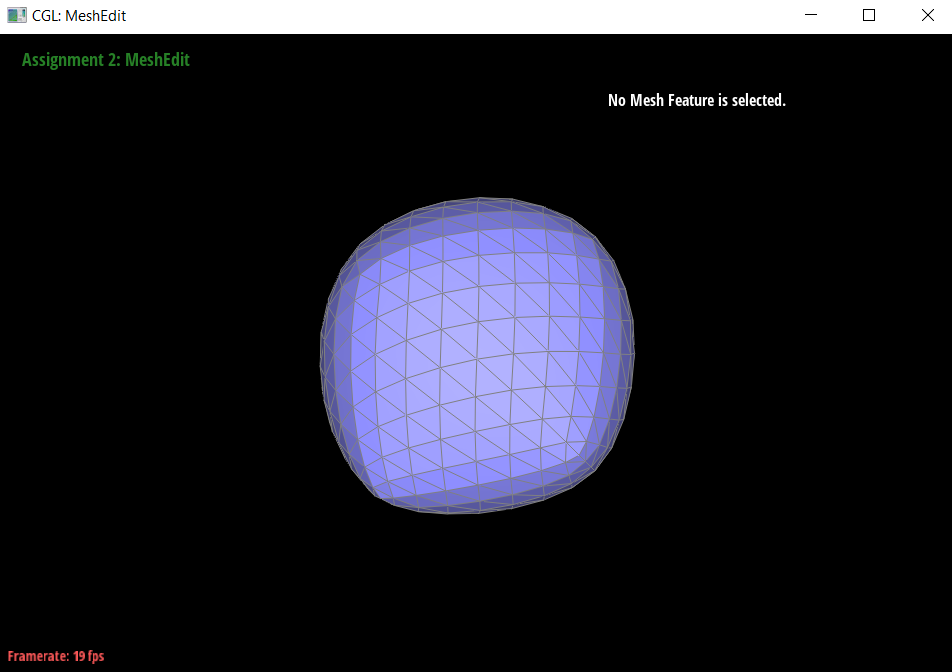
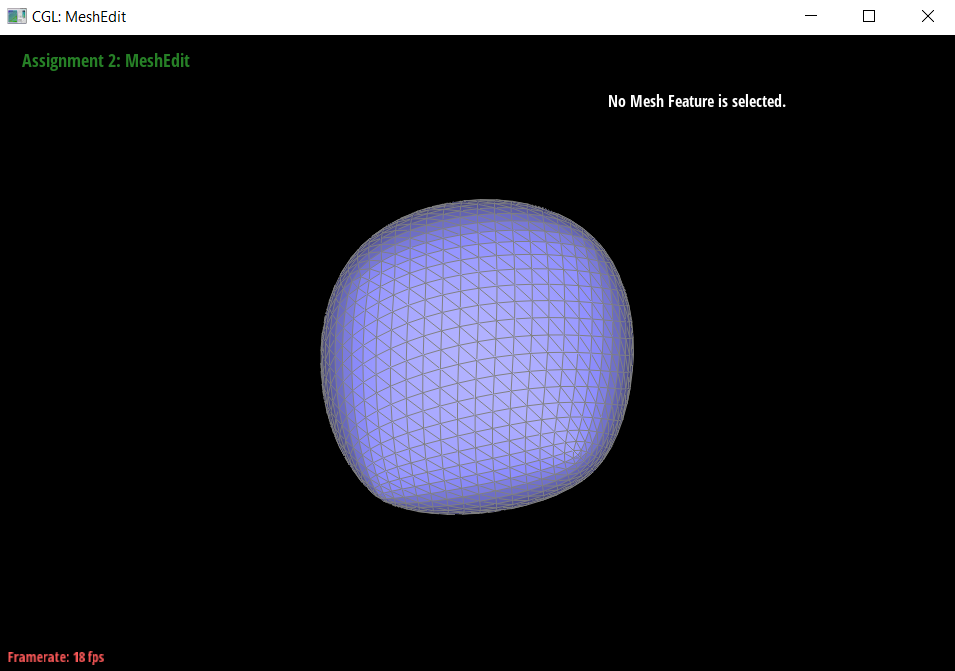
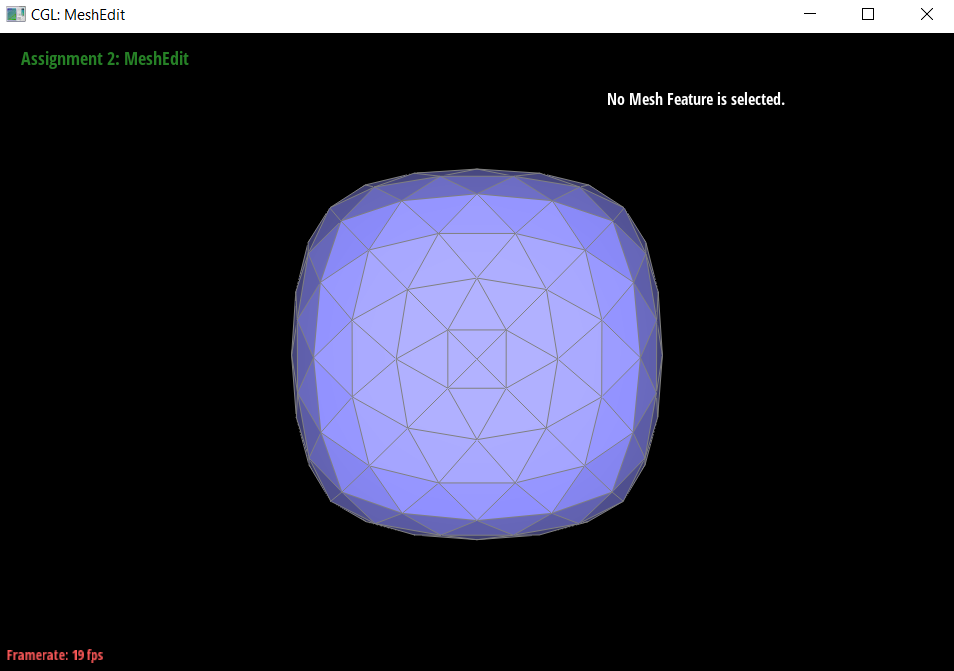
Task 6

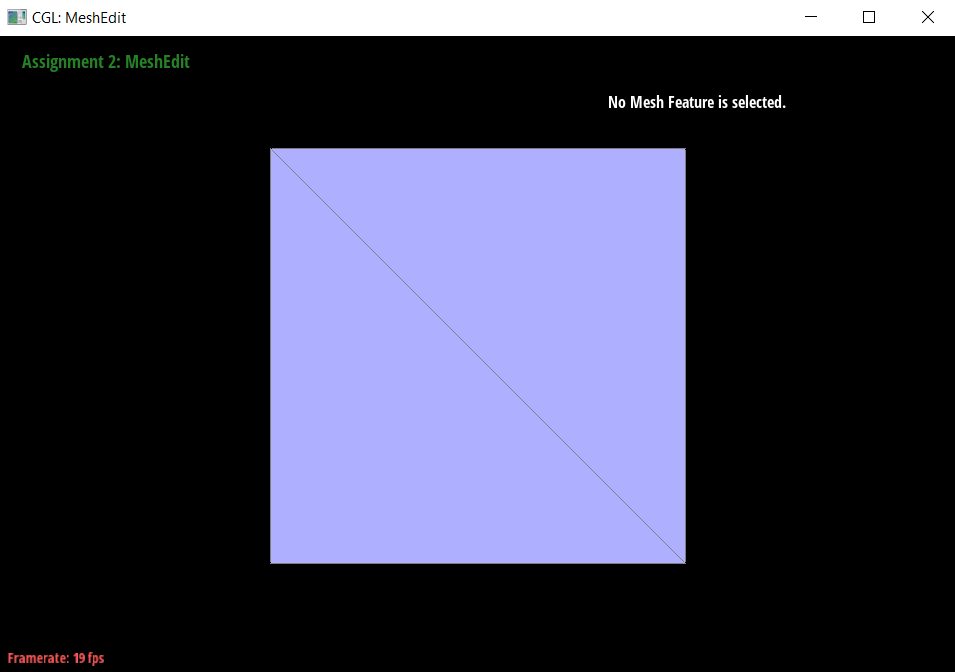
To implement loop subdivision, I followed the steps in the spec which is summarized as follows:

• Iterate through all the original vertices, and find the new vertex value by calculating the degree of the vertex, and the weight of u. I then stored it into the newPosition field.
• Iterate through all the original edges, and compute the position of the new vertex that would get split during the subdivision, and also save this in the newPosition field, but for the edge this time.
• Call splitEdge() on each original edge, ensuring that the isNew value for each newly created edge is true. Also make sure to set the position of the new vertex position to that stored value from part 2.
• Iterate through each newly created edge, and call flipEdge() if the edge is connected to an original vertex and a new vertex.
• Copy the precomputed newPosition values onto the vertex’s actual position value.

No Subdivision	1 Iteration of Subdivision
2 Iterations of Subdivision	3 Iterations of Subdivision
4 Iterations of Subdivision	5 Iterations of Subdivision

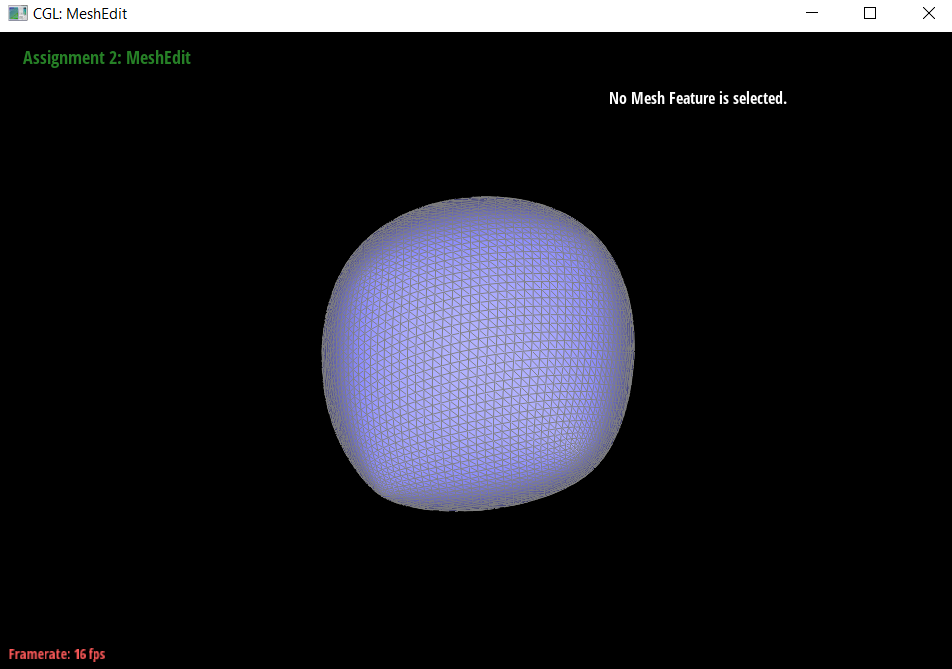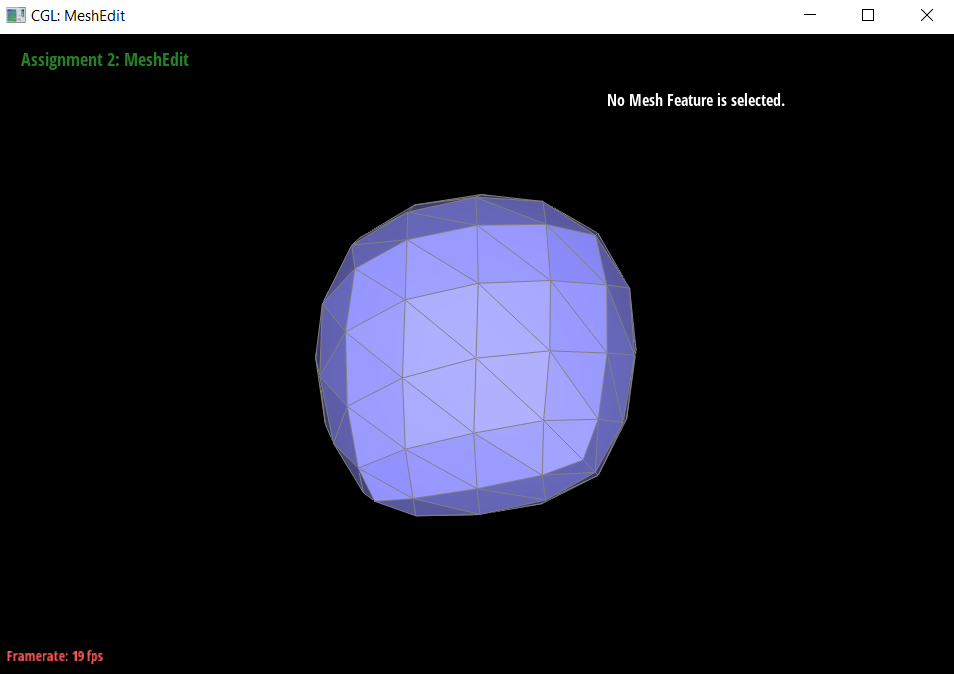
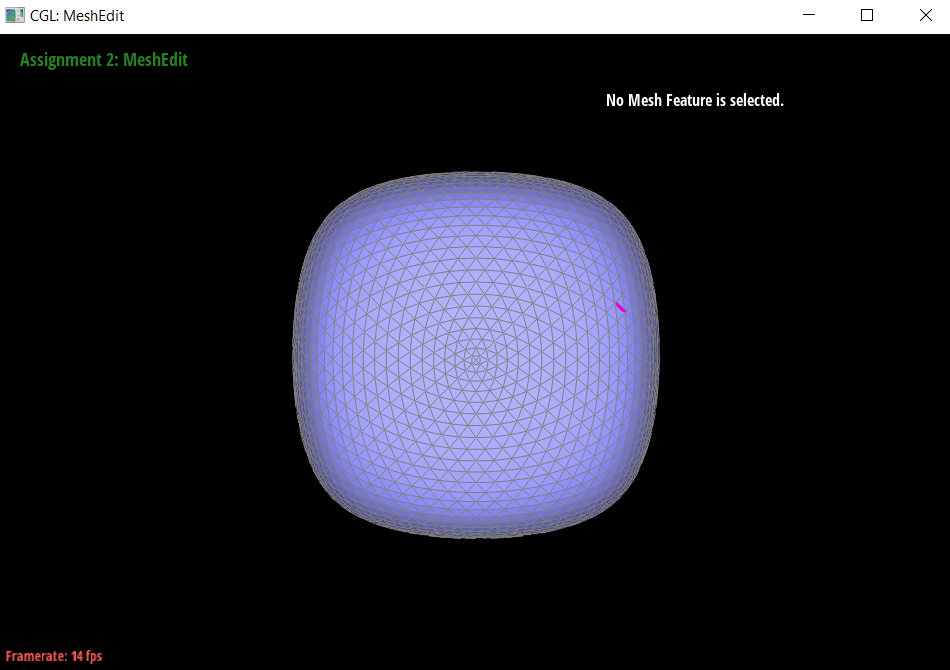
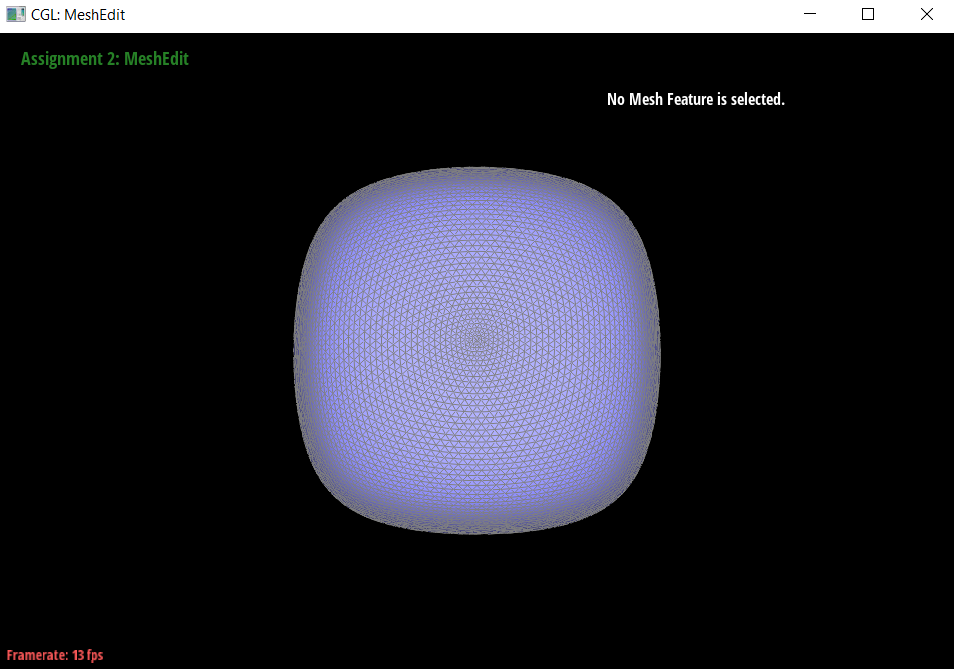
I noticed (which you can see on the cube above) that sharp corners and edges are smoothed out, which is not necessarily always desired. It should still look like a cube after subdivision, not a weird, assymetrical, semi-spherical blob shape.

• This could be remedied by making sure that each face is identical, making it non-assymetric.

No Subdivision with identical faaces	1 Iteration of Subdivision
2 Iterations of Subdivision	3 Iterations of Subdivision
4 Iterations of Subdivision	5 Iterations of Subdivision